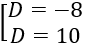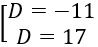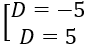Viết phương trình mặt phẳng P song song và cách mặt phẳng Q một khoảng k - Toán lớp 12
Viết phương trình mặt phẳng P song song và cách mặt phẳng Q một khoảng k
Với Viết phương trình mặt phẳng P song song và cách mặt phẳng Q một khoảng k Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình mặt phẳng P song song và cách mặt phẳng Q một khoảng k từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Phương pháp giải
1. Trên mặt phẳng (Q) chọn một điểm M
2. Do mặt phẳng (P) song song với mặt phẳng (Q) nên mặt phẳng (P) có dạng: Ax +By +Cz +D' =0 (D'≠D).
3. Sử dụng công thức khoảng cách d((P),(Q)) =d(M,(Q)) =k để tìm D’.
Ví dụ minh họa
Bài 1: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): x+2y-2z+1=0 và cách (Q) một khoảng bằng 3.
Hướng dẫn:
Trên mặt phẳng (Q) chọn điểm M (-1; 0;0)
Do mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng: x +2y -2z +D =0 (D≠1).
Vì khoảng cách giữa 2 mặt phẳng (P) và (Q) bằng 3 nên ta có:
d(M;(Q))=3 ⇔ 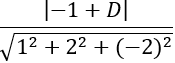
⇔ |-1+D|=9 ⇔
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là
x +2y -2z +10 =0
x +2y -2z -8 =0
Bài 2: Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): 2x+3y-z+3=0 và cách (P) một khoảng bằng √14
Hướng dẫn:
Trên mặt phẳng (Q) chọn điểm M (0; -1;0)
Do mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng: 2x +3y -z +D =0 (D≠3).
Vì khoảng cách giữa 2 mặt phẳng (P) và (Q) bằng √14 nên ta có:
d(M;(Q))=√14 ⇔ 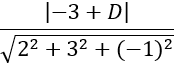
⇔ |-3 +D|=14 ⇔
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là
x +2y -2z +14 =0
x +2y -2z -11 =0
Bài 3: Viết phương trình mặt phẳng (P) song song với mặt phẳng Oxy và cách mặt phẳng Oxy một khoảng bằng 5.
Hướng dẫn:
Điêm O(0; 0; 0) thuộc mặt phẳng Oxy.
Mặt phẳng (P) song song với mặt phẳng Oxy nên mặt phẳng (P) có dạng:
z+D=0 (D≠0)
Do khoảng cách từ mặt phẳng (P) đến mặt phẳng Oxy bằng 5 nên ta có:
d(M;(Q))=5 ⇔ |D|/√(12)=5
⇔ |D|=5 ⇔
Vậy có 2 phương trình mặt phẳng (P) thỏa mãn yêu cầu đề bài là
z +5 =0
z -5 =0