Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức
Câu hỏi:
Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức
A. 19.
B. 13.
C. 14.
D. 15.
Trả lời:
Chọn D.
Ta có:
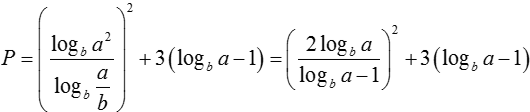
Đặt t = logba – 1 > logbb – 1 = 0; khi đó:
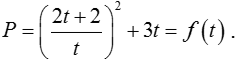
Ta có: 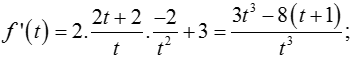
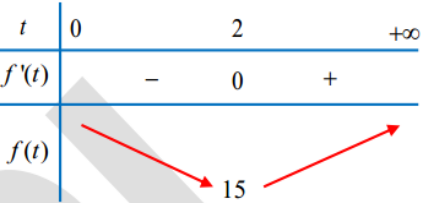
Và f’(t) = 0 khi 3t3 - 8( t + 1) = 0 hay t = 2.
Suy ra Pmin = f(2) = 15
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
Kết quả rút gọn của biểu thức là:
Xem lời giải »
Câu 3:
Cho a; b > 0, Nếu viết thì xy bằng bao nhiêu ?
Xem lời giải »
Câu 4:
Thu gọn biểu thức ta được:
Xem lời giải »
Câu 5:
Cho log9x = log12y = log16 (x + y). Giá trị của tỉ số x/y là:
Xem lời giải »
Câu 6:
Cho x; y > 0 thỏa mãn log2x + log2y = log4( x + y) Tìm x; y để biểu thức P = x2 + y2 đạt giá trị nhỏ nhất.
Xem lời giải »
Câu 7:
Cho với b> a > 1 và P = log2ab + 54logba. Khi đó giá trị của m để P đạt giá trị nhỏ nhất là?
Xem lời giải »
Câu 8:
Cho a; b; c lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c - b và c + b khác 1. Khi đó logc+ba + logc-ba bằng:
Xem lời giải »

