Xét các số thực x,y thỏa mãn 2^x^2+y^2+1<=(x^2+y^2-2x+2).4^x. Giá trị nhỏ nhất của biểu thức P=8x+4/2x-y+1 gần nhất
Câu hỏi:
Xét các số thực x,y thỏa mãn 2x2+y2+1≤(x2+y2−2x+2).4x . Giá trị nhỏ nhất của biểu thức P=8x+42x−y+1 gần nhất với số nào dưới đây
A. 1
B. 2
C. 3
D. 4
Trả lời:
Chọn C
Nhận xét x2+y2−2x+2>0∀x;y
Bất phương trình 2x2+y2+1≤(x2+y2−2x+2).4x⇔2x2+y2+122x≤(x2+y2−2x+2) .
⇔2x2+y2−2x+1≤(x2+y2−2x+2)
Đặt t=x2+y2−2x+1
Bất phương trình ⇔2t≤t+1⇔2t−t−1≤0
Đặt f(t)=2t−t−1 . Ta thấy f(0)=f(1)=0 .
Ta có f'(t)=2tln2−1
f'(t)=0⇔2tln2=1⇔t=log2(1ln2)≈0,52
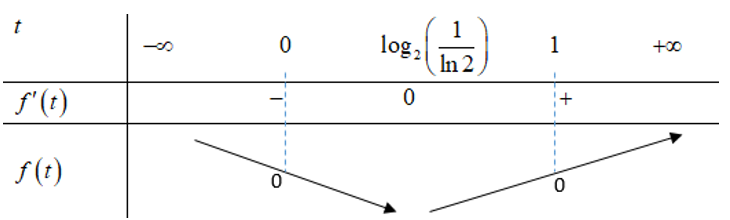
Quan sats BBT ta thấy f(t)≤0⇔0≤t≤1
0≤x2+y2−2x+1≤1⇔(x−1)2+y2≤1(1)
Xét P=8x+42x−y+1⇔2Px−Py+P=8x+4
⇔P−4=(8−2P)x+Py⇔P−4+2P−8=(8−2P)x+2P−8+Py
⇔3P−12=(8−2P)(x−1)+Py
⇔(3P−12)2=[(8−2P)(x−1)+Py]2≤[(8−2P)2+P2][(x−1)2+y2]
Thế vào ta có (3P−12)2≤[(8−2P)2+P2]⇔4P2−40P+80≤0⇔5−√5≤P≤5+√5 .
Dấu “=” xảy ra khi {8−2PP=x−1y=−2√5(x−1)2+y2=1⇔{x−1=−2√5y(−2√5y)2=1⇔{x−1=−2√5yy=±√53⇔[{x=13y=√53{x=53y=−√53
Vậy giá trị nhỏ nhất của là 5−√5≈2,76 gần giá trị 3 nhất.
