Có bao nhiêu cặp số nguyên dương (m,n) sao cho m+n<=12 và ứng với mỗi cặp (m,n) tồn tại đúng 3 số thực 3 thỏa mãn a thuộc (-1,1) ?

Có bao nhiêu cặp số nguyên dương $(m,n)$  sao cho $m+n\le 12$  và ứng với mỗi cặp $(m,n)$  tồn tại đúng 3 số thực $a\in (-1,1)$  thỏa mãn  $2a^m=n\ln (a+\sqrt{a^2+1})$  ?

Chọn D

Ta có $2a^m=n\ln (a+\sqrt{a^2+1})\iff \frac{2}{n}{a}^m=\ln (a+\sqrt{a^2+1})(*)$ .

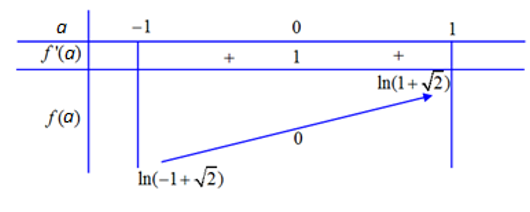
Xét hàm $f\left(a\right)=\ln (a+\sqrt{a^2+1})$  trên $(-1,1)$  (dễ thấy hàm f lẻ, đồng biến trên R), có BBT:

Xét hàm $g\left(a\right)=\frac{2}{n}.a^m$  trên $(-1,1)$  .

Với m chẵn, $g\left(a\right)$   là hàm chẵn và $g\left(a\right)\ge 0,\forall a\in R$ , do đó $(*)$  không thể có 3 nghiệm.

Với m lẻ, $g\left(a\right)$  là hàm lẻ, đồng biến trên  và tiếp tuyến của đồ thị tại điểm a=0 là đường thẳng y=0.

Dễ thấy $(*)$  có nghiệm $a=0\in (-1;1)$ . Để $(*)$  có đúng 3 nghiệm tức là còn có 2 nghiệm nữa là $\pm a_0$  với $0<a_0<1$ .

Muốn vậy, thì $g\left(1\right)=\frac{2}{n}{.1}^m=\frac{2}{n}>f\left(1\right)=\ln (1+\sqrt{2})\iff n<\frac{2}{\ln (1+\sqrt{2})}\approx 2,26\Rightarrow n=1;n=2$

Cụ thể:

+ $m\in \left\{3;5;7;9\right\}$  thì $n\in \left\{1;2\right\}$ : Có 8 cặp $(m,n)$

+ $m=11$  thì : $n\in \left\{1\right\}$ Có  cặp $(m,n)$

+ $m=1$ : Đồ thị hàm số $g\left(a\right)$  là đường thẳng ($g\left(a\right)=a;g\left(a\right)=2a$) không thể cắt đồ thị hàm số $f\left(a\right)$  tại giao điểm $a_0\ne 0$  được vì tiếp tuyến của hàm số $f\left(a\right)$  tại điểm có hoành độ $a=0$  là đường thẳng $y=a$ .

Vậy có cả thảy 9 cặp $y=a$