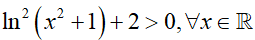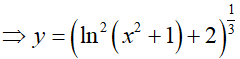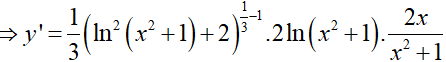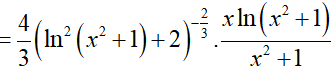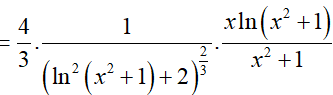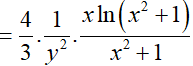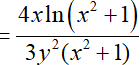Bài tập Hàm số lũy thừa trong đề thi Đại học có lời giải (2 dạng) - Toán lớp 12

---

Bài tập Hàm số lũy thừa trong đề thi Đại học có lời giải (2 dạng)

Với Bài tập Hàm số lũy thừa trong đề thi Đại học có lời giải (2 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hàm số lũy thừa từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1. Tìm tập xác định của hàm số

1. Phương pháp giải

Cho hàm số lũy thừa y = [f(x)]^α :

+ Nếu α nguyên dương thì hàm số xác định với mọi x ∈ R.

+ Nếu α nguyên âm hoặc α = 0 thì hàm số xác định với mọi x ≠ 0.

+ Nếu α không nguyên thì hàm số xác định với mọi x > 0

2. Ví dụ minh họa

Ví dụ 1. Tìm tập xác định D của hàm số y = (x² − 3x + 2)¹⁰⁰ .

A. D = [1; 2]    B. D = [2; + ∞) ∪ (−∞; 1)

C. D = R.    D. D = (1; 2)

Lời giải:

Đáp án: C

Hàm số với α nguyên dương, xác định với ∀x ∈ R .

Do đó hàm số y = (x² − 3x + 2)¹⁰⁰ xác định với ∀x ∈ R .

Ví dụ 2. Tìm tập xác định D của hàm số y = (x³ − 8)⁻¹⁰⁰ .

A. D = (2; +∞)    B. D = R\ {2}

C. D = (−∞; 2)    D. D = (−2; +∞) ∪ (−∞; 2)

Lời giải:

Đáp án: B

Hàm số y = x^α với α nguyên âm, xác định với ∀x ≠ 0 .

Hàm số y = (x³ − 8)⁻¹⁰⁰ xác định x³ − 8 ≠ 0 ⇔ x ≠ 2.

Ví dụ 3. Tìm tập xác định D của hàm số y = (x³ − 8)⁰

A. D = (2; +∞)    B. D = R\{2}

C. D = (−∞; 2)    D. D = (−2; +∞) ∪ (−∞; 2)

Lời giải:

Đáp án: B

Hàm số y = x^α với α = 0 xác định với ∀x ≠ 0 .

Hàm số y = (x³ − 8)⁰ xác định ⇔ x³ − 9 ≠ 0 ⇔ x³ ≠ 8 ⇔ x ≠ 2.

Ví dụ 4. Tìm tập xác định D của hàm số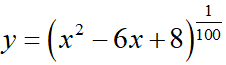

A. D = R    B. D = [4; +∞) ∪ (−∞; 2)

C. D = (4; +∞) ∪ (−∞; 2)    D. D = [2;4]

Lời giải:

Đáp án: C

Hàm số y = x^α với α không nguyên , có tập xác định là tập số thực dương.

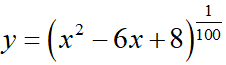
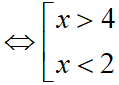
Hàm số xác định x² − 6x + 8 > 0

Do đó, tập xác định của hàm số đã cho là D = (4; +∞) ∪ (−∞; 2)

Ví dụ 5. Tìm tập xác định D của hàm số y = (x² −6x + 8)^√2

A. D = R    B. D = [4; +∞) ∪ (−∞; 2)

C. D = (4; +∞) ∪ (−∞; 2)    D. D = [2;4]

Lời giải:

Đáp án: C

Hàm số y = x^α với α không nguyên , có tập xác định là tập số thực dương.

Hàm số y = (x² −6x + 8)^√2 xác định x² − 6x + 8 > 0

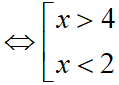
Do đó, tập xác định của hàm số đã cho là D = (4; +∞) ∪ (−∞; 2)

Dạng 2. Tính đạo hàm của hàm số lũy thừa

1. Phương pháp giải

a. Hàm số lũy thừa y = x^α có (α ∈ R) đạo hàm tại mọi điểm x > 0 và (x^α)' = αx^{α − 1}

b. Nếu hàm số u = u(x) nhận giá trị dương và có đạo hàm trên J thì y = u^α(x) cũng có đạo hàm trên J và (u^α(x))' = α . u^{α − 1}(x) . u'(x)

2. Ví dụ minh họa

Ví dụ 1. Tính đạo hàm của hàm số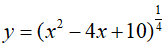

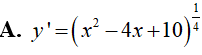
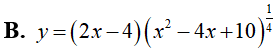
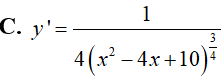
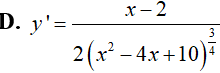
Lời giải:

Đáp án: D

Ta có:

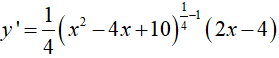
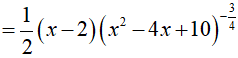
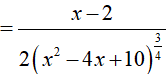
Ví dụ 2. Tính đạo hàm của hàm số y= (x³ + 4x² + 2√x ). e^x

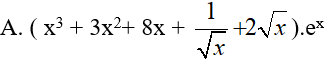
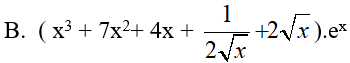
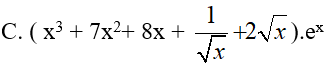
Lời giải:

Đáp án: C

Ta có:

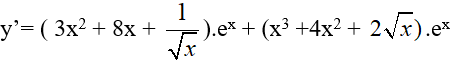
Hay

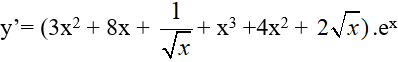
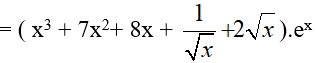
Ví dụ 3. Tính đạo hàm của hàm số y = √(3² −2x + 1)

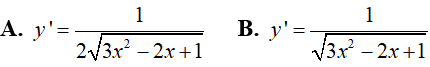
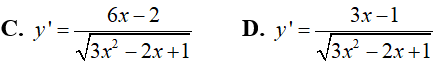
Lời giải:

Đáp án: D

Ta có:

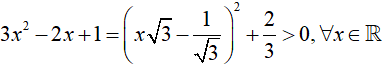
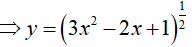
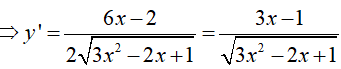
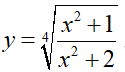
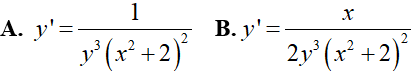
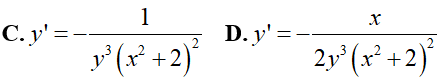
Ví dụ 4. Cho hàm số . Mệnh đề nào dưới đây là đúng?

Lời giải:

Đáp án: B

Ta có:

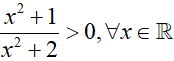
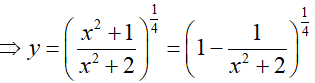
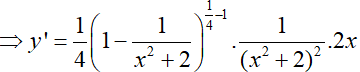
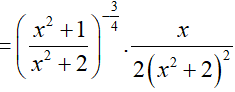
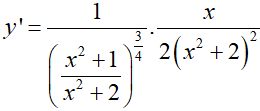
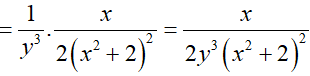
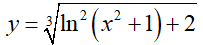
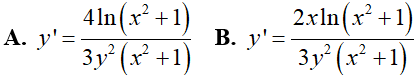
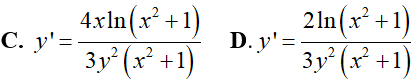
Ví dụ 5. Cho hàm số . Mệnh đề nào dưới đây là đúng?

Lời giải:

Đáp án: B

Ta có: