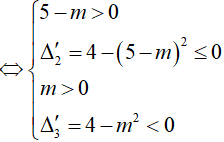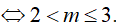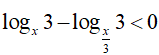Bài tập Bất phương trình logarit trong đề thi Đại học có lời giải (5 dạng) - Toán lớp 12

---

Bài tập Bất phương trình logarit trong đề thi Đại học có lời giải (5 dạng)

Với Bài tập Bất phương trình logarit trong đề thi Đại học có lời giải (5 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Bất phương trình logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1. Tìm điều kiện xác định của bất phương trình lôgarit

1. Phương pháp giải

Biểu thức loga f(x) xác định khi:

+ a > 0; a ≠ 1

+ f(x) > 0 và f(x) có nghĩa.

2. Ví dụ minh họa

Ví dụ 1. Điều kiện xác định của bất phương trình 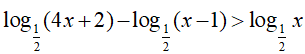là

Lời giải:

Đáp án: C

Bất phương trình xác định khi:

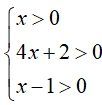
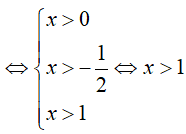
Ví dụ 2. Điều kiện xác định của bất phương trình 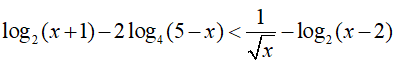là

A. 2 < x < 5    B. 1 < x < 2.    C. 2 < x < 3    D. −4 < x < 3

Lời giải:

Đáp án: A

Bất phương trình xác định khi:

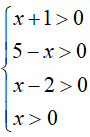
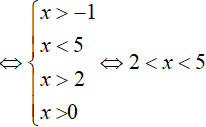
Ví dụ 3. Điều kiện xác định của bất phương trình 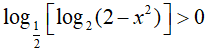là

A. x ∈ [−1; 1] .    B. x ∈ (−1; 0) ∪ (0; 1) .

C. x ∈ (−1; 1) ∪ (2; +∞).    D. x ∈ (−1; 1).

Lời giải:

Đáp án: D

Bất phương trình xác định khi:

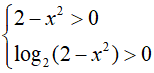
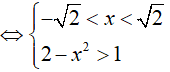
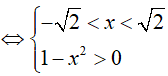
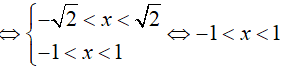
Dạng 2. Giải bất phương trình lôgarit bằng phương pháp đưa về cùng cơ số

1. Phương pháp giải

Cho bất phương trình log_ax < m với x > 0 (1)

+ Nếu 0 < a < 1 thì (1) x > a^m.

+ Nếu a > 1 thì (1) x < a^m

Chú ý: Kết hợp với điều kiện xác định khi giải bất phương trình.

2. Ví dụ minh họa

Ví dụ 1. Giải bất phương trình: log₅ (x − 2) + 2log₂₅ x > log₅3.

Lời giải:

Đáp án: C

Điều kiện:

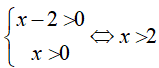
Với điều kiện trên, bất phương trình trở thành:

log₅ (x − 2) + log₅x > log₅3

⇔ log₅ ( x − 2).x > log₅3 ⇔ (x − 2).x > 3

⇔ x² − 2x − 3 > 0

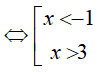
Kết hợp với điều kiện ta được, x > 3

Ví dụ 2. Nghiệm nguyên nhỏ nhất của bất phương trình log₂(log₄x) ≥ log₄(log₂x) là:

A. 6.    B. 10.    C. 8.    D. 16.

Lời giải:

Đáp án: D

BPT

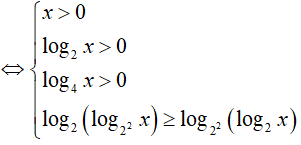
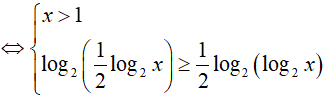
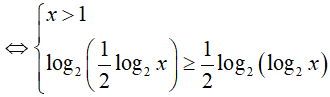
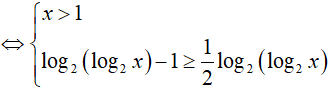
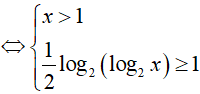
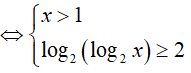
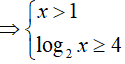
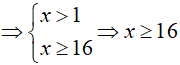
Ví dụ 3. Nghiệm nguyên nhỏ nhất của bất phương trình 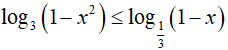là:

Lời giải:

Đáp án: A

BPT

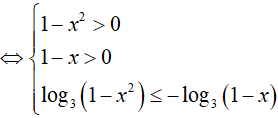
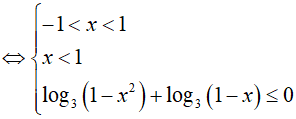
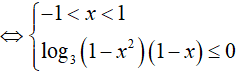
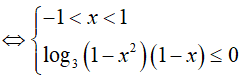
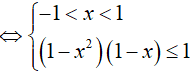
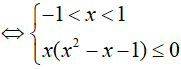
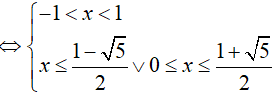
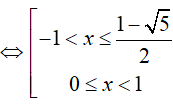
Do đó, x = 0 là nghiệm nguyên nhỏ nhất.

Ví dụ 4. Bất phương trình log_x(log₃(9^x − 72)) ≤ 1 có tập nghiệm là:

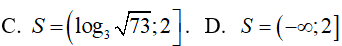
Lời giải:

Đáp án: A

+ Điều kiện : log₃ (9^x − 72) > 0 ⇔ 9^x − 72 > 1

⇔ 9^x > 73 ⇔ x > log₃√73

+ Với điều kiện trên ta có :

log_x(log₃(9^x − 72)) ≤ 1 ⇔ log₃(9^x − 72) < x ⇔ 9^x − 3^x − 72 ≤ 0; (*)

Đặt t = 3^x ; (t > 0). Khi đó, bất phương trình (*) trở thành :

t² − t − 72 < 0 ⇔ − 8 < t < 9

Kết hợp điều kiện t > 0 nên 0 < t < 9.

Suy ra, 0 < 3^x < 9 ⇔ x < 2.

Kết hợp điều kiện, tập nghiệm của bất phương trình đã cho là: S = [log₃√73; 2] .

Ví dụ 5. Giải bất phương trình

Lời giải:

Đáp án: C

Điều kiện : x > 0; x ≠ 1; x ≠ 3

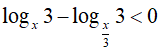
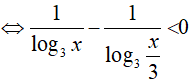
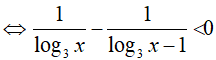
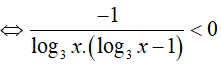
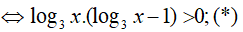
Đặt t = log₃x thì (*) trở thành: t ( t-1) > 0

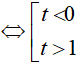
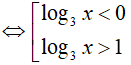
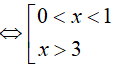
Dạng 3. Giải bất phương trình lôgarit bằng phương pháp đặt ẩn phụ

2. Ví dụ minh họa

Ví dụ 1. Bất phương trình log_0,2²x − 5log_0,2x < −6 có tập nghiệm là:

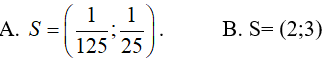
Lời giải:

Đáp án: A

Điều kiện: x > 0

Đặt t = log_0,2x. Khi đó, bất phương trình đã cho trở thành:

t² − 5t < − 6 ⇔ t² − 5t + 6 < 0 hay 2 < t < 3.

Khi đó, ta có: 2 < log_0,2x < 3 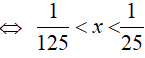( thỏa mãn điều kiện).

Ví dụ 2. Giải bất phương trình log₃(4 . 3^{x − 1}) > 2x − 1 :

Lời giải:

Đáp án: A

Bất phương trình đã cho luôn xác định với mọi x.

Ta có: log₃ (4. 3^x−1) > 2x − 1

⇔ 4.3^{x − 1} > 3^{2x − 1} ⇔ 3^2x − 4. 3^x < 0 (*)

Đặt t = 3^x ( t > 0). Khi đó, phương trình (*) trở thành:

t² − 4t < 0 ⇔ 0 < t < 4

suy ra, 0 < 3^x < 4 ⇔ x < log₃4

Ví dụ 3. Nếu đặt t =log2x thì bất phương trình 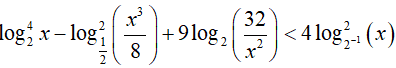trở thành bất phương trình nào?

A. t⁴ +13t² + 36 < 0 .    B. t⁴ + 12t² + 12 < 0

C. t⁴ < 24t² + 23 > 0    D. t⁴ − 13t² + 36 < 0

Lời giải:

Đáp án: D

Điều kiện: x > 0.

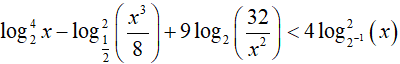
⇔ log₂⁴x − (−log₂x³ + log₂8)² + 9(log₂32 − log₂x²) < 4log₂²x

⇔ log₂⁴x − (3log₂x − 3)² + 9(5 − 2log₂x) − 4log₂²x < 0

⇔ log₂⁴x − (9log₂²x − 18log₂x + 9) + 45 − 18log₂x − 4log₂² < 0

⇔ log₂⁴x − 13log₂²x + 36 < 0

Đặt t= log₂x khi đó phương trình trên trở thành :

t⁴ − 13t² + 36 < 0

Ví dụ 4. Tập nghiệm của bất phương trình 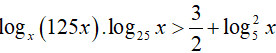là

Lời giải:

Đáp án: A

Điều kiện: 0 < x ≠ 1 (*)

Ta có:

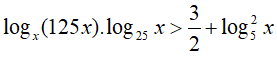
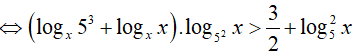
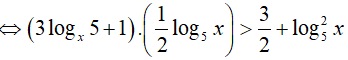
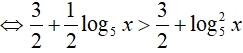
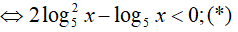
Đặt t = log₅x, khi đó (*) trở thành: 2t² − t < 0

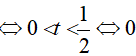
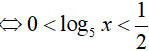
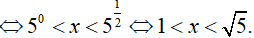
(thỏa mãn điều kiện)

Vậy tập nghiệm của bất phương trình đã cho là S = (1; √5) .

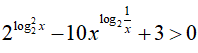
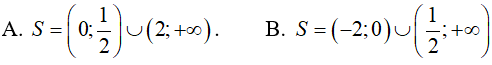
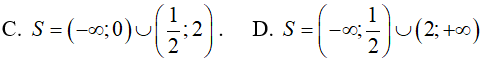
Ví dụ 5. Tập nghiệm của bất phương trình là

Lời giải:

Đáp án: A

Điều kiện: x > 0 (*). Đặt u = log₂x => x = 2^u

Bất phương trình đã cho trở thành

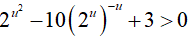
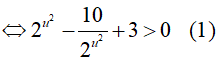
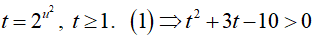
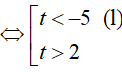
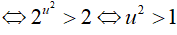
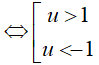
- Với u > 1 => log₂x > 1 => x > 2

- Với u < −1 => log₂x < −

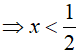
Kết hợp điều kiện (*), ta được nghiệm của bất phương trình đã cho là x > 2 hoặc

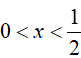
Dạng 4. Giải bất phương trình lôgarit bằng phương pháp đánh giá, tính đơn điệu của hàm số.

1. Phương pháp giải

a. Phương pháp đánh giá:

Để giải bất phương trình: A( x) < B(x) ta có thể chứng minh với mọi x < x0 ta có A(x) ≥ B(x)

và mọi x ≥ x₀ thì A(x)< B(x).

Khi đó, nghiệm của bất phương trình đã cho là x ≥ x₀

b. Tính đơn điệu của hàm số

Cho hàm số y = f(x) xác định trên khoảng D. Giả sử hàm số y= f(x) đơn điệu trên khoảng D.

+ Nếu hàm số y = f(x) đồng biến trên D thì f(x) > f(x0 ) ⇔ x > x₀.

+ Nếu hàm số y = f(x) nghịch biến trên D thì f(x) > f(x0)  ⇔ < x₀.

2. Ví dụ minh họa

Ví dụ 1. Bất phương trình log₂(2^x + 1) + log₃(4^x + 2) ≤ 2 có tập nghiệm là:

A. [0; +∞).    B. (−∞; 0).    C. (−∞; 0].    D. (0; +∞) .

Lời giải:

Đáp án: C

* Xét x > 0 => 2^x > 2⁰ = 1 => 2^x + 1 > 2

Suy ra, log₂ (2^x +1) > log₂2 = 1 (1)

* Khi x > 0 thì 4^x > 4⁰ = 1 => 4^x + 2 > 2 + 1= 3

Suy ra, log₃ (4^x + 2) > log₃3 = 1 ( 2)

* Cộng vế với vế của (1) và (2) ta được: log₂ (2^x + 1) + log₃ ( 4^x + 2) > 2

Mà BPT: log₂(2^x + 1) + log₃(4^x + 2) ≤ 2 nên x > 0 ( loại) .

* Xét x ≤ 0

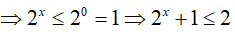
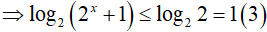
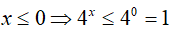
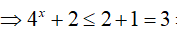
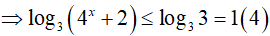
Cộng vế với vế của (3) và (4) ta được: log₂(2^x + 1) + log₃(4^x + 2) ≤ 2 (tm)

Vậy x ≤ 0 hay x ∈ (−∞; 0]

Ví dụ 2. Giải bất phương trình: log₃ (2^x + 1) + x ≤ 2

Lời giải:

Đáp án: B

Điều kiện:

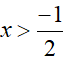
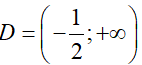
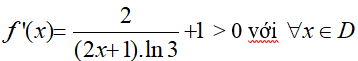
Xét hàm số y = f(x) = log₃(2^x + 1) + x trên có đạo hàm:

Suy ra, hàm số đồng biến trên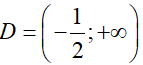

Khi đó, log₃ (2^x + 1) + x ≤ 2 ⇔ f(x) ≤ f(1) ⇔ x ≤ 1

Kết hợp với điều kiện , ta có nghiệm của bất phương trình đã cho là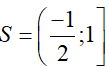

Ví dụ 3. Giải bất phương trình log₂(3^x + 7) + log₃(4^x + 11) ≥ 7

Lời giải:

Đáp án: C

Tập xác định D = R.

Xét hàm số y = log₂(3^x + 7) + log₃(4^x + 11) xác định và liên tục trên R.

Đạo hàm

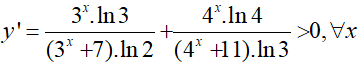
Suy ra, hàm số đồng biến trên R.

Do đó, bất phương trình đã cho trở thành: f(x) ≥ f(2) = 7 ⇔ x ≥ 2

Vậy tập nghiệm của bất phương trình là [2; +∞)

Ví dụ 4. Giải bất phương trình −log₅(3^x + 16) − 2x < −6.

Lời giải:

Đáp án: A

Tập xác định D = R.

Đặt f(x) = −log₅(3^x + 16) − 2x liên tục và xác định trên R.

Đạo hàm

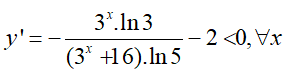
Do đó, hàm số y= f(x) nghịch biến trên R. Khi đó, bất phương trình đã cho trở thành; f(x) < f(2) ⇔ x > 2.

Vậy tập nghiệm của bất phương trình là (2; +∞)

Dạng 5. Bất phương trình logarit có chứa tham số m

2. Ví dụ minh họa

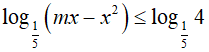
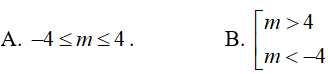
Ví dụ 1. Tìm tất cả giá trị thực của tham số m để bất phương trình vô nghiệm?

Lời giải:

Đáp án: D

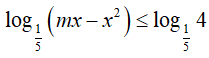
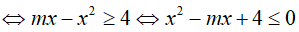
Để bất phương trình đã cho vô nghiệm khi và chỉ khi bất phương trình: x² − mx + 4 ≤ 0 vô nghiệm

⇔ x² − mx + 4 > 0 ∀x ∈ R ⇔ Δ = m² − 16 < 0 ⇔ −4 < m < 4

Ví dụ 2. Tìm tất cả các giá trị thực của tham số m để bất phương trình log₂(5^x − 1). log₂(2.5^x − 2) ≥ m có nghiệm x ≥ 1 ?

A. m ≥ 6.    B. m > 6    C. m ≤ 6.    D. m < 6

Lời giải:

Đáp án: C

BPT

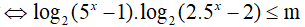
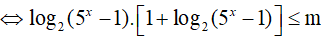
Đặt 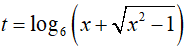do x ≥ 1 => t ∈ [2; +∞)

BPT

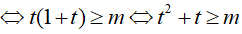
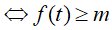
Với f(t) = t² + t có f’(t) = 2t + 1 > 0 với t ∈ [2; +∞) nên hàm đồng biến trên t ∈ [2; +∞)

Nên min f(t) = f(2) = 6.

Do đó để để bất phương trình log₂(5^x − 1). log₂(2.5^x − 2) ≥ m có nghiệm x ≥ 1 thì :

m ≤ Minf(t) ⇔ m < 6

Ví dụ 3. Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log₅ (x² + 1) > log₅ (x² +4x + m) − 1.

Lời giải:

Đáp án: A

Ta có: log₅ (x² + 1) > log₅ (x² +4x + m) − 1

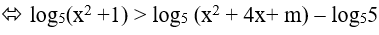
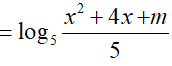
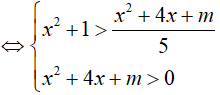
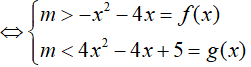
Hệ trên thỏa mãn ∀x ∈ (2; 3)

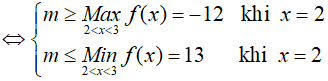
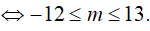
Ví dụ 4. Tìm tất cả các giá trị thực của tham số m để bất phương trình log₂(7x² + 7) ≥ log₂(mx² + 4x + m), ∀x ∈ R

Lời giải:

Đáp án: C

Bất phương trình tương đương : 7x² + 7 ≥ mx² + 4x + m > 0, ∀x ∈ R

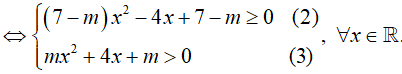
Nếu m = 7 thì (2) không thỏa ∀x ∈ R

Nếu m =0 thì (3) không thỏa ∀x ∈ R

Do đó, để (1) thỏa ∀x ∈ R

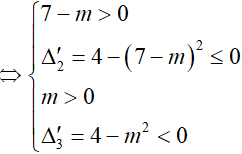
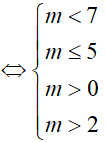
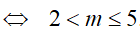
Ví dụ 5. Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log₅(x² + 1) ≥ log₅(mx² + 4x + m) có nghiệm đúng mọi x.

Lời giải:

Đáp án: A

Bất phương trình tương đương : 5(x² + 1) ≥ mx² + 4x + m > 0, ∀x ∈ R

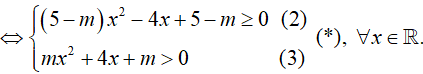
Nếu m = 0 hoặc m= 5 : (*) không thỏa ∀x ∈ R

m ≠ 0 và m ≠ 5: (*)