Bài tập Phương trình logarit trong đề thi Đại học có lời giải (5 dạng) - Toán lớp 12

---

Bài tập Phương trình logarit trong đề thi Đại học có lời giải (5 dạng)

Với Bài tập Phương trình logarit trong đề thi Đại học có lời giải (5 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1. Tìm điều kiện xác định của phương trình lôgarit.

1. Phương pháp giải

Cho phương trình log_af(x) = g(x).

Điều kiện xác định của phương trình là:

+ a > 0; a ≠ 1

+ f(x) > 0 và f(x) có nghĩa

+ g(x) có nghĩa.

2. Ví dụ minh họa

Ví dụ 1. Điều kiện xác định của phươg trình log_2x+2 156 = 24 là:

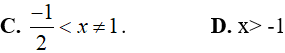
Lời giải:

Đáp án: B

Điều kiện xác định của phương trình: log_{2x + 2} 156 = 24

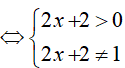
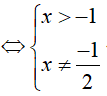
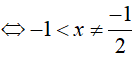
Ví dụ 2. Điều kiện xác định của phươg trình log_x(2x² − 7x − 12) là:

A. x ∈ (0; 1) ∪ (1: +∞)    B. x ∈ (−∞; 0) .    C. x ∈ (0; 1) .    D. x ∈ (0; +∞)

Lời giải:

Đáp án: A

Phương trình log_x(2x² − 7x − 12) xác định:

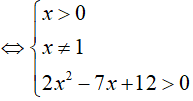
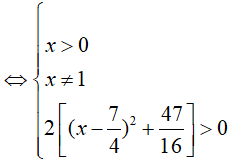
⇔x ∈ (0; 1) ∪ (1: +∞)

Ví dụ 3. Điều kiện xác định của phương trình 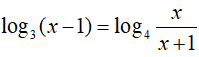là:

A. x ∈ (1; +∞).    B. x ∈ (−1; 0).    C. x ∈ R\[−1; 0].    D. x ∈ (−∞; 1).

Lời giải:

Đáp án: A

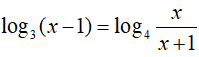
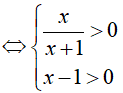
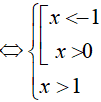
Điều kiện xác định của phương trình đã cho là: Biểu thức log₃(x − 1) và xác định

⇔ x > 1

Ví dụ 4. Điều kiện xác định của phương trình 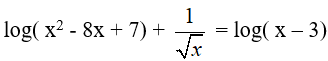là:

A. 0 < x < 7    B. x > 7    C. 3 < x < 7    D. 0 < x < 3

Lời giải:

Đáp án: B

Điều kiện phương trình:

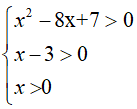
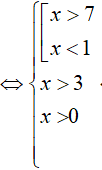
⇔ x > 7

Ví dụ 5. Điều kiện xác định của phương trình log₂[3log₂(3x − 1) − 1] là:

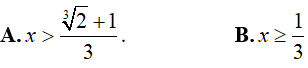
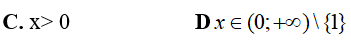
Lời giải:

Đáp án: A

Biểu thức log₂[3log₂(3x − 1) − 1] = x xác định khi và chỉ khi:

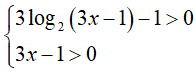
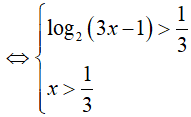
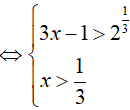
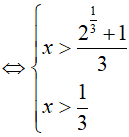
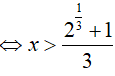
Dạng 2. Giải phương trình logarit bằng phương pháp đưa về cùng cơ số.

1. Phương pháp giải

Thường áp dụng các phép tính lôgarit để biến đổi, để hóa đồng cơ số hoặc để khử biểu thức lôgarit chứa ẩn số ta thường lấy mũ các vế. Ta áp dụng các công thức

Với a > 0; a ≠ 1

• log_a M = log_a N ⇔ M = N > 0

• log_a f(x) = log_a g(x)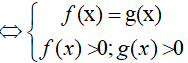

• log_a N = M ⇔ N= a^M hoặc log_a f(x)= b ⇔ f(x) = a^b

Ngoài ra, cần chú ý đến một số tính chất

• log_ab có nghĩa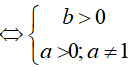

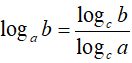
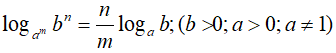
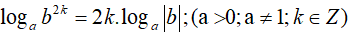
• (công thức đổi cơ số).

2. Ví dụ minh họa

Ví dụ 1. Phương trình 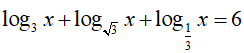có nghiệm là:

A. x = 27    B. x = 9    C. x = 3    D. x = log₃6

Lời giải:

Đáp án: A

Điều kiện x > 0

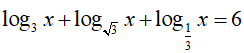
⇔ log₃x + 2log₃x − log₃x = 6

2log₃x = 6 ⇔ log₃x = 3 ⇔ x = 27

Ví dụ 2. Phương trình 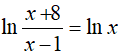có nghiệm là:

A. x= − 2     B. x = 4 hoặc x = −2 .    C. x = 4    D. x = 1

Lời giải:

Đáp án: C

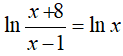
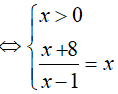
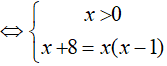
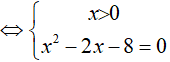
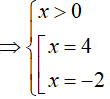
⇔ x = 4

Ví dụ 3. Số nghiệm của phương trình log₄ (x + 12). log_x2 = 1 là:

A. 0.    B. 2.    C. 3.    D. 1.

Lời giải:

Đáp án: D

Điều kiện : 0 < x ≠ 1

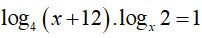
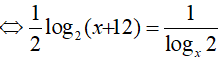
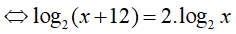
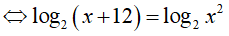
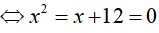
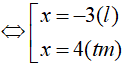
Vậy phương trình đã cho có 1 nghiệm là x=4.

Ví dụ 4. Phương trình log_{2x − 3}(3² − 7x + 3) − 2 = 0 có nghiệm là:

A. x = 2; x= 3    B. x= 2    C. x= 3    D. x= 1, x= 5

Lời giải:

Đáp án: D

Điều kiện:

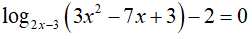
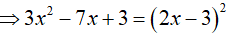
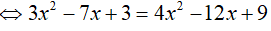
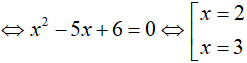
Kết hợp với điều kiện, ta có nghiệm phương trình là x= 3

Ví dụ 5. Số nghiệm nguyên dương của phương trình 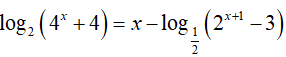là:

A. 2.    B. 1.    C. 3.    D. 0.

Lời giải:

Đáp án: B

Điều kiện: 2^{x + 1} − 3 > 0 ⇔ x > log₂3 − 1

Ta có:

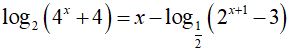
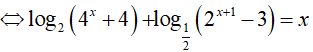
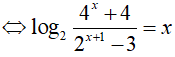
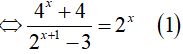
Đặt t = 2^x(t > 0)

Ta có

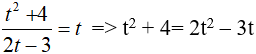
⇔ t² − 3t − 4 = 0 => t = 4

Do đó, 2^x = 4 ⇔ x = 2 (thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là x = 2.

Ví dụ 6. Số nghiệm của phương trình log₄(log₂x) + log₂(log₄x) = 2 là:

A. 0.    B. 2.    C. 3.    D. 1.

Lời giải:

Đáp án: D

Phương trình đã cho tương đương:

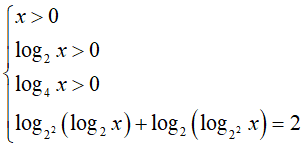
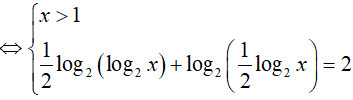
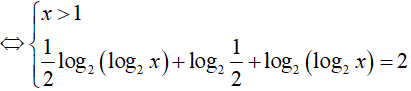
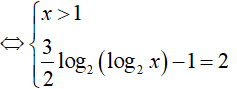
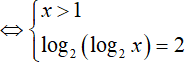
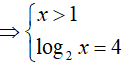
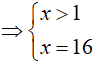
=> x = 16

Dạng 3. Giải phương trình lôgarit bằng phương pháp đặt ẩn phụ

2. Ví dụ minh họa

Ví dụ 1. Phương trình log₂²x − 4log₂x + 3 = 0 có tổng các nghiệm là:

A. 6    B. 8    C. 2    D. 10

Lời giải:

Đáp án: D

Điều kiện: x > 0

Đặt log₂ x= t. Khi đó, phương trình đã cho trở thành

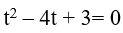
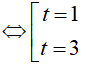
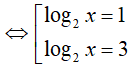
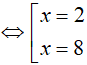
Kết hợp với điểu kiện, phương trình đã cho có 2 nghiệm là x= 2 và x= 8.

Tổng các nghiệm của phương trình là: S = 2 + 8 =10

Ví dụ 2. Gọi x₁, x₂ là 2 nghiệm của phương trình 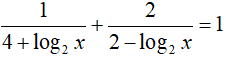. Khi đó x₁ + x₂ bằng:

Lời giải:

Đáp án: D

Điều kiện

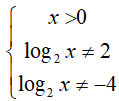
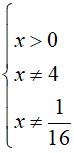
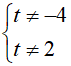
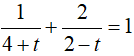
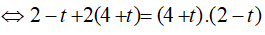
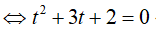
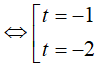
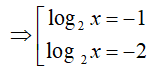
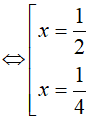
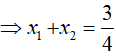
Đặt t = log₂x, điều kiện . Khi đó phương trình trở thành:

Ví dụ 3. Phương trình log₅²(2x − 1) − 8log₅√(2x − 1) + 3 = 0 có tổng các nghiệm là:

A. 4    B. 10    C. 26    D. 66

Lời giải:

Đáp án: D

Điều kiện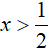

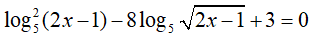
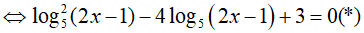
Đặt t= log₅ (2x − 1). Khi đó, phương trình (*) trở thành:

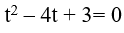
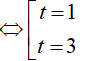
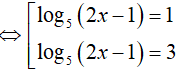
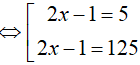
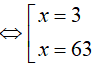
Do đó, tổng các nghiệm của phương trình đã cho là: 63 + 3= 66.

Ví dụ 4. Biết phương trình 4^log₉x − 6.2^log₉x + 2^log₃27 = 0 có hai nghiệm x₁; x₂. Khi đó x₁² + x₂² bằng

Lời giải:

Đáp án: A

Điều kiện: x > 0

Ta có phương trình tương đương 2^2log₉x − 6.2^2log₉x + 2³ = 0 (1)

Đặt t = 2^log₉x, t > 0. (1) => t² − 6t + 8 = 0 ⇔ t = 2 hoặc t = 4

- Với t = 2 ⇔ 2^log₉x = 2 ⇔ log₉x = 1 ⇔ x = 9

- Với t = 4 ⇔ 2^log₉x = 2² ⇔ log₉x = 2 ⇔ x = 81.

Vậy tập nghiệm của phương trình đã cho là S = {9; 81} => x₁² + x₂² = 6642 .

Ví dụ 5. Tập nghiệm của phương trình 4^log₂2x − x^log₂6 = 2.3^log₂4x2 là:

Lời giải:

Đáp án: C

Điều kiện: 0 < x ≠ 1

Ta có:

4^log₂2x − x^log₂6 = 2.3^log₂4x2

⇔ 4^{1 + log₂x} − 6^log₂x = 2.3^2+2log₂x

⇔ 4.4^log₂x − 6^log₂x = 19.9^log₂x (1)

Chia 2 vế cho 4^log₂x.

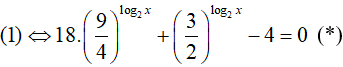
Đặt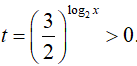

Khi đó, phương trình (*) trở thành:

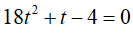
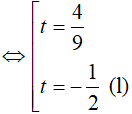
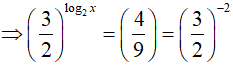
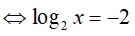
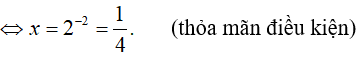
Vậy tập nghiệm của phương trình đã cho là .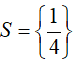

Dạng 4. Giải phương trình lôgarit bằng phương pháp đưa về phương trình tích

1. Phương pháp giải

Để giải phương trình lôgarit ta có thể đặt nhân tử chung, dùng hằng đẳng thức đáng nhớ.... để đưa phương trình đã cho về dạng A(x). B(x) = 0

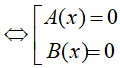
2. Ví dụ minh họa

Ví dụ 1. Nghiệm nhỏ nhất của phương trình − log_√3(x − 2). log₅x = 2log₃(x − 2) là:

Lời giải:

Đáp án: B

Điều kiện: x > 2

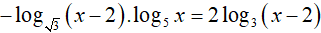
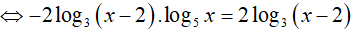
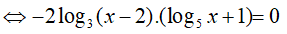
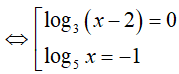
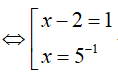
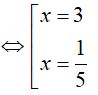
So điều kiện suy ra phương trình có nghiệm x= 3.

Ví dụ 2. Số nghiệm của phương trình log₂x . log₃(2 − 1) = 2log₂x là:

A. 2.    B. 0.    C. 1.    D. 3.

Lời giải:

Đáp án: A

PT

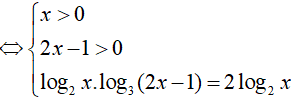
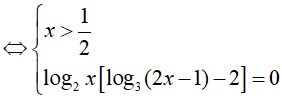
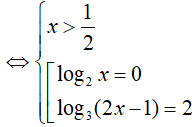
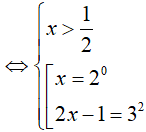
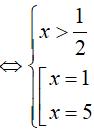
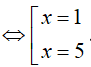
So điều kiện suy ra phương trình có nghiệm x= 3.

Ví dụ 3. Cho hàm số f(x)= 3x³lnx − 36x. lnx − 7x³ + 108x tập nghiệm của phương trình f’(x)= 0 là.

Lời giải:

Đáp án: A

Điều kiện: x > 0

Ta có:

f'(x) = 9²lnx + 3x² − 36lnx − 36 − 21x² + 108 = 0

⇔ 9(x² − 4)lnx − 18(x² − 4) = 0

⇔ 9(x² − 4)(lnx − 2) = 0

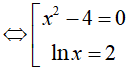
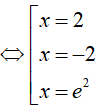
Kết hợp với điều kiện ta có nghiệm của phương trình đã cho là S= {e²; 2}.

Dạng 5. Tìm tham số m thỏa mãn điều kiện T.

2. Ví dụ minh họa

Ví dụ 1. Tìm tất cả các giá trị thực của tham số m để phương trình log₃x − log₃(x − 2) = log_√3m có nghiệm?

A. m > 1.    B. m ≥ 1.    C. m < 1    D. m ≤ 1.

Lời giải:

Đáp án: A

Điều kiện: x > 2 và m > 0.

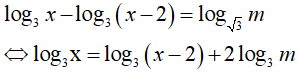
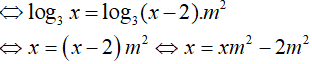
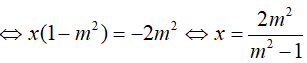
Phương trình có nghiệm x > 2 khi đó:

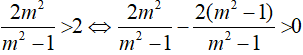
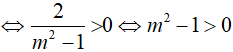
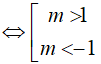
Kết hợp điều kiện m > 0 ta được m > 1 .

Ví dụ 2. Tìm tất cả các giá trị thực của tham số m để phương trình 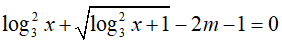có ít nhất một nghiệm thuộc đoạn [1; 3^√3] ?

A. m ∈ [0; 2].    B. m ∈ (0; 2).    C. m ∈ (0; 2].    D. m ∈ [0; 2).

Lời giải:

Đáp án: A

Với x ∈ [1; 3^√3] hay 1 ≤ x ≤ 3^√3

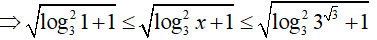
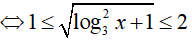
Đặt t = √(log₃²x + 1); t ∈ [1; 2]

Phương trình đã cho trở thành: t² − 1 + t − 2m − 1 = 0 hay t² + t − 2= 2m

Khi đó bài toán trở thành:Tìm m để phương trình t² + t − 2 = 2m có ít nhất một nghiệm thuộc đoạn [1; 2].

Xét hàm số f(t) = t² + t − 2, ∀t ∈ [1; 2], f'(t) = 2t + 1 > 0, ∀t ∈ [1; 2]

Suy ra hàm số đồng biến trên [1; 2].

Ta có bảng biến thiên của hàm số.

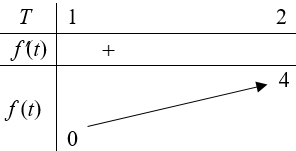
Khi đó phương trình có nghiệm khi 0 ≤ 2m ≤ 4 ⇔ 0 ≤ m ≤ 2

Vậy 0 ≤ m ≤ 2 là các giá trị cần tìm.

Ví dụ 3. Tìm tất cả các giá trị của tham số m để phương trình log₂(5^x − 1).log₄(2.5^x − 2 ) = m có nghiệm x ≥ 1 ?

A. m ∈ [2; +∞).    B. m ∈ [3; +∞).    C. m ∈ (−∞; 2].    D. m ∞ (−∞; 3].

Lời giải:

Đáp án: B

Ta có: log₂(5^x − 1).log₄(2.5^x − 2 )

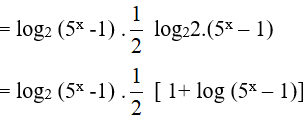
Đặt t = log₂ (5^x − 1). Khi đó, phương trình đã cho trở thành:

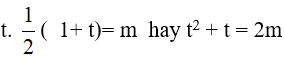
Với x ≤ 1 => 5^x ≤ 5 => log₂(5^x − 1) ≤ log₂(5 − 1)hay t ≥ 2 .

Khi đó bài toán trở thành: Tìm m để phương trình t² + t = 2m có nghiệm

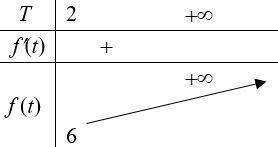
Xét hàm số f(t) = t² + t, ∀t ≥ 2, f'(t) = 2t + 1 > 0, ∀t ≥ 2

Suy ra hàm số đồng biến với t ≥ 2.

Khi đó phương trình có nghiệm khi 2m ≥ 6 ⇔ m ≥ 3

Vậy m ≥ 3 là các giá trị cần tìm.

Ví dụ 4. Tìm tất cả các giá trị thực của tham số m để phương trình log₃²x − (m + 2)log₃x + 3m − 1 = 0 có hai nghiệm x1; x2 thỏa mãn x₁.x₂ = 27?

A. m = −2    B. m = −    C. m = 1    D. m = 27

Lời giải:

Đáp án: C

Đặt t = log₃x. Khi đó phương trình có dạng: t² − (m + 2).t + 3m − 1 = 0 (1).

Để phương trình có hai nghiệm phân biệt thì

Δ = (m + 2)² − 4(3m − 1) = m² − 8m + 8 > 0

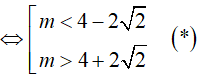
Với điều kiện (*), phương trình (1) có 2 nghiệm t1 ; t2 và :

t₁ + t₂ = log₃x₁ + log₃x₂ = log₃ (x₁.x₂) = log₃27 = 3

Theo Vi-ét ta có: t₁ + t₂ = m + 2. Do đó, m+ 2 = 3 ⇔ m= 1 (thỏa mãn điều kiện)

Vậy m = 1 là giá trị cần tìm.

Ví dụ 5. Tìm tất cả các giá trị thực của tham số m để phương trình 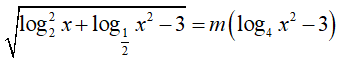có nghiệm thuộc [32; +∞)?

A. m ∈ (1; √3].    B. m ∈ [1; √3).    C. m ∈ [−1; √3).    D. m ∈ (−√3; 1]

Lời giải:

Đáp án: C

Điều kiện: x > 0.Khi đó phương trình tương đương:

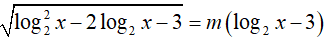
Đặt t = log₂x với x ≥ 32 => log₂x ≥ log₂32 = 5 hay t ≥ 5

Phương trình đã cho trở thành : √(t² − 2t − 3) = m(t − 3) (*).

Khi đó bài toán trở thành : Tìm m để phương trình (*) có nghiệm t ≥ 5 ”

Với t ≥ 5 thì (*)

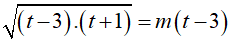
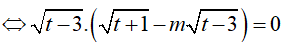
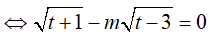
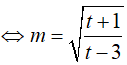
Ta có:

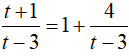
Với

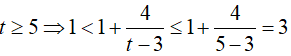
hay

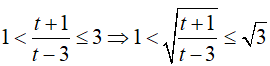
Suy ra 1 < m ≤ √3 Vậy phương trình có nghiệm với 1 < m ≤ √3