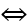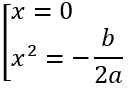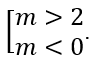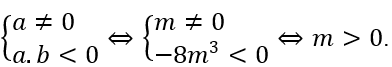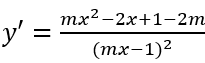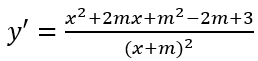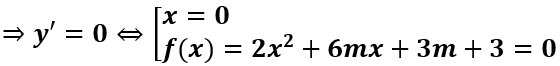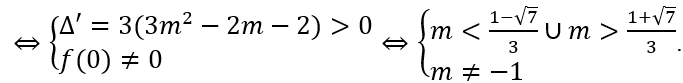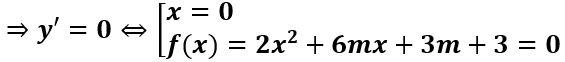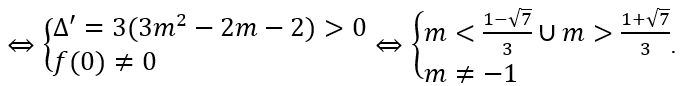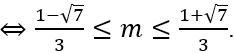Biện luận theo m số cực trị của hàm số cực hay - Toán lớp 12

Biện luận theo m số cực trị của hàm số cực hay

Với Biện luận theo m số cực trị của hàm số cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Biện luận theo m số cực trị của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Phương pháp giải

1. Cực trị của hàm số bậc ba

Cho hàm số y = ax³ + bx² + cx + d, a ≠ 0.

y' = 0 ⇔ 3ax² + 2bx + c = 0 (1) ; Δ'_y' = b² - 3ac

    Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.

    Hàm số bậc 3 không có cực trị ⇔ b² - 3ac ≤ 0

    Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.

     Hàm số bậc 3 có 2 cực trị ⇔ b² - 3ac > 0

2. Cực trị của hàm số bậc bốn trùng phương

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

y' = 4ax³ + 2bx; y' = 0 ⇔

    (C)có một điểm cực trị y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

    (C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Ví dụ minh họa

Ví dụ 1: Tìm m để hàm số y = x³ + mx + 2 có cả cực đại và cực tiểu.

Hướng dẫn

y' = 3x² + m.

Hàm số y = x³ + mx + 2 có cả cực đại và cực tiểu khi và chỉ khi y'= 0 có hai nghiệm phân biệt.

Vậy m < 0.

Ví dụ 2: Cho hàm số y = (m - 2)x³ - mx - 2. Với giá trị nào của m thì hàm số có cực trị?

Hướng dẫn

Tập xác định D = R.

Tính y' = 3(m - 2)x² - m.

Cho y' = 0 ⇔ 3(m - 2)x² - m = 0   (1).

   + TH1: Xét m = 2 ⇒ y' = -2 < 0 ∀ x nên hàm số đã cho không có cực trị.

   + TH2: Xét m ≠ 2

Hàm số có cực trị khi Δ'> 0 ⇔ m(m - 2) > 0 ⇔

Vậy m > 2 ∨ m < 0.

Ví dụ 3: Xác định các giá trị của tham số m để đồ thị hàm số y = mx⁴ - m² x² + 2016 có 3 điểm cực trị?

Hướng dẫn

Tập xác định D = R.

Tính y' = 4mx³ - 2xm².

Để hàm số có 3 điểm cực trị khi

B. Bài tập vận dụng

Bài 1: Tìm m để hàm số y = mx³ + 3mx² - (m - 1)x - 1 có cực trị.

Lời giải:

TXĐ: D = R

Ta có: y' = 3mx² + 6mx - m + 1. Hàm số có đạo hàm tại mọi điểm nên x₀ là điểm cực trị của hàm số thì đạo hàm tại đó phải bằng 0.

Vậy hàm số có cực trị khi và chỉ khi y' = 0 phải có nghiệm và y' đổi dấu qua nghiệm đó.

         * Nếu m = 0 ⇒ y' = 1 > 0 ∀ x ∈ R ⇒ hàm số không có cự trị

         * Nếu m ≠ 0. Khi đó y' là một tam thức bậc hai nên y' = 0 có nghiệm và đổi dấu khi qua các nghiệm 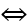y' = 0 có hai nghiệm phân biệt hay Δ' = 12m² - 3m > 0 ⇔ m < 0 hoặc m > 1/4.

Vậy, với m < 0 hoặc m > 1/4 là những giá trị cần tìm.

Bài 2: Tìm m để hàm số y = x³ - 3(m - 1)x² + 3(2m - 4)x + m có cực trị.

Lời giải:

Ta có: y' = 3[x² - 2(m - 1)x + 2m - 4]

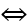
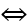
Hàm số có cực trị y' = 0 có hai nghiệm phân biệt Δ' = m² - 4m + 5 > 0 đúng với mọi m. Vậy hàm số luôn có cực trị với mọi m.

Bài 3: Tìm điều kiện của tham số m để hàm số y = x³ + mx² +(4m + 3)x + 2m - 1 có hai điểm cực trị.

Lời giải:

Tập xác định D = R.

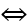
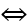
Tính y' = 3x² + 2mx + 4m + 3; Hàm số có hai cực trị y' = 0 có hai nghiệm thực phân biệt và đổi dấu Δ' > 0 ⇔ m² - 12m - 9 > 0 (khi đó y' đổi dấu qua nghiệm) ⇔ m ∈(-∞;6-3√5)∪(6+3√5;+∞).

Bài 4: Tìm các giá trị của m để hàm số y = x³ - 2mx + 4 không có điểm cực trị.

Lời giải:

         * Tập xác định D = R.

         * Tính y' = 3x² - 2m.

         * Hàm số không có điểm cực trị khi phương trình y' = 0 vô nghiệm hoặc có nghiệm kép 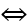x² = 2m/3 ≤ 0 ⇔ m ≤ 0.

Bài 5: Tìm m để hàm số 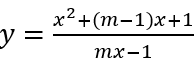có cực trị.

Lời giải:

      • Với m = 0 ta có y = -x² + x - 1, ta thấy hàm số đạt cực đại tại x = 1/2. Suy ra m = 0 thỏa yêu cầu bài toán.

      • m ≠ 0, ta có:

Suy ra y' = 0 ⇔ mx² - 2x + 1 - 2m = 0 (*)

Hàm số đã cho có cực trị khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác 1/m ⇔ 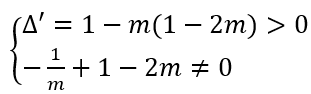⇔2m² - m + 1 > 0 đúng với mọi m.

Vậy hàm số đã cho luôn có cực trị với mọi m.

Bài 6:Tìm m để hàm số 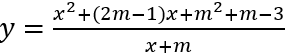có cực trị.

Lời giải:

Ta có:

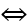
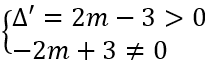
Hàm số có cực đại, cực tiểu phương trình x² + 2mx + m² - 2m + 3 = 0 có hai nghiệm phân biệt khác -m ⇔ ⇔ m > 3/2.

Bài 7:Tìm m để hàm số y = x⁴ + 4mx³ + 3(m + 1)x² + 1 có ba cực trị

Lời giải:

Ta có y' = 4x³ + 12mx² + 6(m + 1)x = 2x(2x² + 6mx + 3(m + 1))

Hàm số có ba cực trị khi và chỉ khi f(x) có hai nghiệm phân biệt khác 0

Bài 8:Tìm m để hàm số y = x⁴ + 4mx³ + 3(m + 1)x² + 1 có cực tiểu mà không có cực đại.

Lời giải:

Ta có y' = 4x³ + 12mx² + 6(m + 1)x = 2x(2x² + 6mx + 3(m + 1))

Hàm số có ba cực trị khi và chỉ khi f(x) có hai nghiệm phân biệt khác 0

Hàm chỉ có cực tiểu mà không có cực đại hàm số có 1 cực trị và a > 0