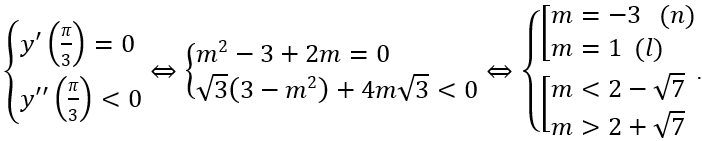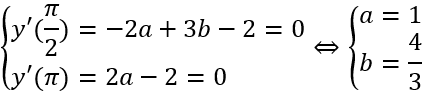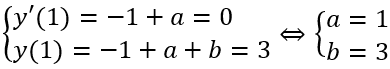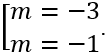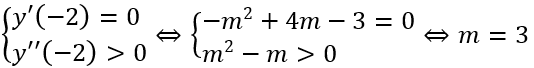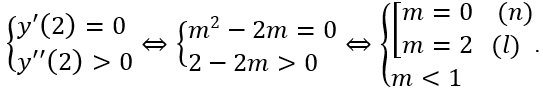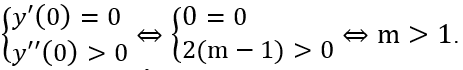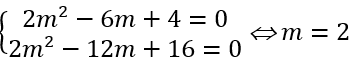Bài tập trắc nghiệm Tìm tham số m để hàm số đạt cực trị tại một điểm cực hay - Toán lớp 12
Bài tập trắc nghiệm Tìm tham số m để hàm số đạt cực trị tại một điểm cực hay
Với Bài tập trắc nghiệm Tìm tham số m để hàm số đạt cực trị tại một điểm cực hay Toán lớp 12 tổng hợp 12 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tham số m để hàm số đạt cực trị tại một điểm từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1. Với giá trị nào của tham số m thì hàm số y = 2(m2 - 3)sinx - 2msin2x + 3m - 1 đạt cực đại tại x = π/3.
A. Không tồn tại giá trị m. B. m = 1.
C. m = -3 D. m = -3, m = 1.
Lời giải:
Đáp án : C
Giải thích :
Tập xác định D = R.
Tính y' = 2(m2 - 3)cosx - 4mcos2x; y'' =2(3 - m2 )sinx + 8msin2x.
Để hàm số đã cho đạt cực đại tại x = π/3 ta có
Vậy m = -3 là giá trị cần tìm.
Câu 2. Tìm tất cả các giá trị của tham số m để hàm số y = x2 - mx2 + (2m - 3)x - 3 đạt cực đại tại x = 1.
A. m = 3. B. m > 3. C. m ≤ 3. D. m < 3.
Lời giải:
Đáp án : B
Giải thích :
+ Để hàm số đạt cực đại x = 1thì 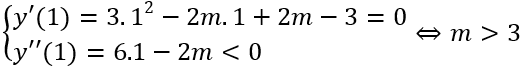
Câu 3. Hàm số y = asin2x + bcos3x - 2x (0 < x < 2π) đạt cực trị tại x = π/2; x = π. Khi đó, giá trị của biểu thức P = a + 3b - 3ab là:
A. 3. B. -1. C. 1. D. -3.
Lời giải:
Đáp án : C
Giải thích :
TXĐ: D = R
+ Ta có: y' = 2acos2x - 3bsin3x - 2.
Hàm số đạt cực trị tại x = π/2; x = π nên ta có hệ phương trình:
Do đó, giá trị của biểu thức P = a + 3b - 3ab = 1.
Câu 4. Hàm số y = x3 - 3x2 + mx - 2 đạt cực tiểu tại x = 2 khi?
A. m > 0. B. m ≠ 0. C. m = 0. D. m < 0.
Lời giải:
Đáp án : C
Giải thích :
y' = 3x2 - 6x + m
y''= 6x - 6 )
Hàm số đạt cực tiểu tại x = 2 khi:
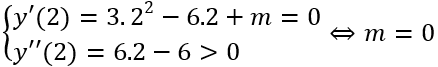
Câu 5. Biết đồ thị hàm số y = x3 - 2x2 + ax + b có điểm cực trị là A(1;3). Khi đó giá trị của 4a - b là:
A. 1. B. 2. C. 3. D. 4.
Lời giải:
Đáp án : A
Giải thích :
Ta có y' = 3x2 - 4x + a
Đồ thị hàm số có điểm cực trị là A(1;3), ta có:
Khi đó ta có, 4a - b = 1.
Câu 6. Tìm tất cả các giá trị thực của tham số mđể hàm số y = 1/3 x3 + (m2 - m + 2)x2 + (3m2 + 1)x đạt cực tiểu tại x = -2.
A. 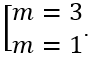
Lời giải:
Đáp án : B
Giải thích :
y' = x2 + 2(m2 - m + 2)x + 3m2 + 1
y'' = 2x + 2(m2 - m + 2))
Hàm số đạt cực tiểu tại x = -2 khi:
Câu 7. Cho hàm số y = 1/3 x3 - (m + 1)x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
A. m = 1. B. m = 0. C. m = 2. D. m = 3.
Lời giải:
Đáp án : B
Giải thích :
Tập xác định D = R.
Tính y' = x2 – 2(m + 1)x + m2 + 2m; y'' = 2x – 2m - 2.
Để hàm số đã cho đạt cực tiểu tại x = 2 ⇒
Vậy m = 0 là giá trị cần tìm.
Câu 8. Tất cả các giá trị thực của tham số m để hàm số y = x4 + (m - 1)x2 + 3 đạt cực tiểu tại
x = 0 là:
A. m ≥ 1. B.m ≤ 1 . C.m > 1. D. m < 1.
Lời giải:
Đáp án : A
Giải thích :
Tập xác định D = R.
Tính y' = 4x3 + 2(m - 1)x; y'' = 12x2 + 2(m - 1).
Để hàm số đã cho đạt cực tiểu tại x = 0 ⇒
Với m = 1, phương trình trở thành y = x4 + 3 đạt cực tiểu tại x = 0
Vậy m ≥ 1 là giá trị cần tìm.
Câu 9. Tìm tất cả các giá trị thực của tham số m để hàm số y = 1/3 x3 - mx2 + (m + 1)x - 1 đạt cực đại tại x = -2 ?
A. Không tồn tại m. B.-1 . C.2. D. 3.
Lời giải:
Đáp án : A
Giải thích :
Tập xác định D = R.
y' = x2 - 2mx + m + 1
y" = 2x - 2m
Hàm số đạt cực đại tại x = -2 khi : 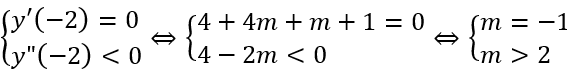
Câu 10. Tìm tất cả các giá trị của m để hàm số y = 1/3 x3 - 1/2 (3m+2)x2 + (2m2 + 3m + 1)x - 4 đạt cực trị tại x = 3 và x = 5, ta được.
A. m = 0. B. m = 1. C. m = 2. D. m = 3.
Lời giải:
Đáp án : C
Giải thích :
Tập xác định D = R.
Tính y' = x2 - (3m + 2)x + 2m2 + 3m + 1; y'' = 2x - (3m + 2).
Để hàm số đã cho đạt cực trị tại x = 3;x = 5 thì
y'(3) = 0 và y'(5) = 0 nên
Thử lại m = 2 thỏa mãn
Câu 11. Cho hàm số y = ax3 + bx2 + cx + d. Nếu đồ thị hàm số có hai hai điểm cực trị là gốc tọa độ O và điểm A(2;-4) thì phương trình của hàm số là:
A. y = -3x3 + x2. B. y = -3x3 + x. C. y = x3 - 3x. D. y = x3 - 3x2.
Lời giải:
Đáp án : D
Câu 12. Hàm số y = ax3 - ax2 + 1 có điểm cực tiểu x = 2/3 khi điều kiện của a:
A. a = 0. B. a > 0. C. a = 2. D. a < 0.
Lời giải:
Đáp án : B
Giải thích :
Tập xác định D = R.
Tính y'= 3ax2 - 2ax; y'' = 6ax - 2a.
Để hàm số đã cho đạt cực tiểu tại x = 2/3 thì