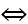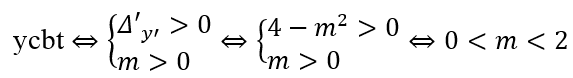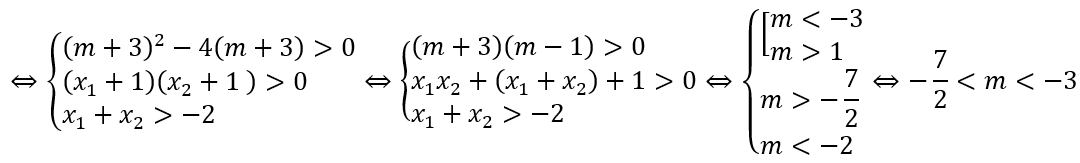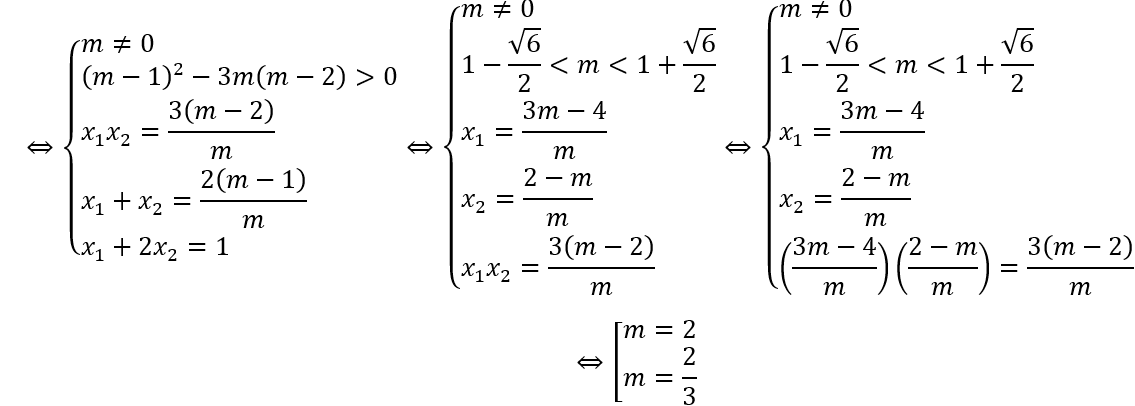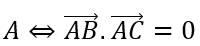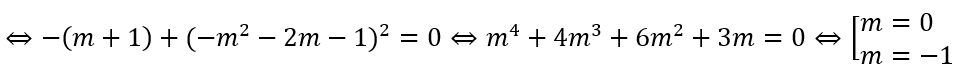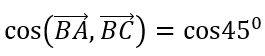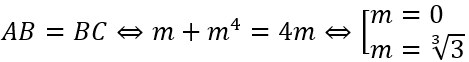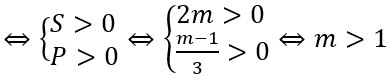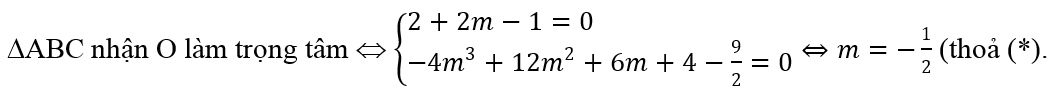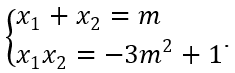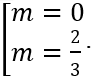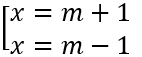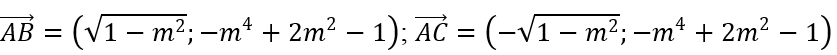Bài tập trắc nghiệm về cực trị hàm số cực hay, có lời giải - Toán lớp 12

---

Bài tập trắc nghiệm về cực trị hàm số cực hay, có lời giải

Với Bài tập trắc nghiệm về cực trị hàm số cực hay, có lời giải Toán lớp 12 tổng hợp 12 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về cực trị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1: Tìm tất cả các giá trị thực của tham số m để hàm số y = m/3 x³ + 2x² + mx + 1 có 2 điểm cực trị thỏa mãn x_CĐ < x_CT.

A. m < 2.    B.-2 < m < 0.    C. -2 < m < 2.    D. 0 < m < 2.

Lời giải:

Đáp án : D

Giải thích :

[Phương pháp tự luận]

y' = mx² + 4x + m

Câu 2: Tìm tất các giá trị thực của tham số m để hàm số y = 1/3 x³ + (m + 3)x² + 4(m + 3)x + m³ - m đạt cực trị tại x₁,x₂ thỏa mãn -1 < x₁ < x₂.

A. -7/2 < m < -2.    B. -3 < m < 1.     C. 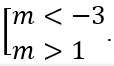    D. -7/2 < m < -3.

Lời giải:

Đáp án : D

Giải thích :

y' = x² + 2(m + 3)x + 4(m + 3)

Yêu cầu của bài toán ⇔ y' = 0 có hai nghiệm phân biệt x₁, x₂ thỏa mãn:

-1 < x₁ < x₂.

Câu 3: Tìm các giá trị của tham sốmđể hàm số: y = 1/3 mx³ - (m - 1)x² + 3(m - 2)x + 1/6 đạt cực trị tại x₁,x₂_2 thỏa mãn x₂ + 2x₂ = 1.

A. 1 - √6/2 < m < 1 + √6/2.     B.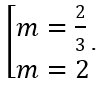

C.m ∈(1 - √6/2; 1 + √6/2) \ {0}.    D. m = 2.

Lời giải:

Đáp án : B

Giải thích :

y' = mx² - 2(m - 1)x + 3(m - 2)

Yêu cầu của bài toán 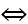y' = 0 có hai nghiệm phân biệt x₁; x₂ thỏa mãn:

x₁ + 2x₂ = 1.

Câu 4: Tìm các giá trị của tham sốm để đồ thị hàm số: y = x⁴ -2m²x² + 1 có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.

A. m = -1.    B. m ≠ 0.    C. m = 1.    D. m = ±1.

Lời giải:

Đáp án : D

Giải thích :

y' = 4x³ - 4m² x

y' = 0 ⇔ 4x(x² - m²) = 0)

Hàm số có 3 điểm cực trị 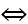m ≠ 0

Khi đó 3 điểm cực trị của đồ thị hàm số là : A(0; 1), B(m; 1 - m⁴ ), C(-m; 1 - m₄ )

Do tính chất đối xứng, ta có ΔABC cân tại đỉnh A .

Vậy ΔABC chỉ có thể vuông cân tại đỉnh

Kết hợp điều kiện ta có: m = ±1 ( thỏa mãn).

Lưu ý: có thể sử dụng công thức b³/8a + 1 = 0.

Câu 5: Tìm các giá trị của tham sốm để đồ thị hàm số: y = x⁴ - 2(m + 1)x² + m² có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.

A. Không tồn tại m.    B. m = 0.    C.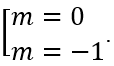    D.m = -1.

Lời giải:

Đáp án : B

Giải thích :

y' = 4x³ - 4(m + 1)x

y' = 0 ⇔ 4x(x² - m - 1) = 0

Hàm số có điểm 3 cực trị 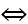m > -1

Khi đó 3 điểm cực trị của đồ thị hàm số là : A(0; m² ), B(-√(m + 1); -2m -1),C(√(m + 1);-2m - 1)

Do tính chất đối xứng, ta có ΔABC cân tại đỉnh A .

Vậy ΔABC chỉ có thể vuông cân tại đỉnh

Kết hợp điều kiện ta có: m = 0 ( thỏa mãn).

Lưu ý: Có thể làm theo cách khác:

+) Cách 1: Gọi M là trung điểm của BC, tìm tọa độ điểm M, ΔABC vuông tại đỉnh A thì 2AM = BC.

+) Cách 2: Sử dụng định lý Pitago BC² = AB² + AC²

+) Cách 3:

+) Hoặc sử dụng công thức b³/8a + 1 = 0

Câu 6: Tìm các giá trị của tham số m để đồ thị hàm số: y = x⁴ - 2mx² + 2m + m⁴ có ba điểm cực trị là ba đỉnh của một tam giác đều.

A. Không tồn tại m.    B.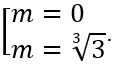     C. m = ∛3.     D. m = ±√3.

Lời giải:

Đáp án : C

Giải thích :

y' = 4x³ - 4mx

y' = 0 ⇔ 4x(x² - m) = 0

Hàm số có 3 cực trị 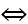m > 0

Khi đó 3 điểm cực trị của đồ thị hàm số là : A(0; m⁴ + 2m),B(-√m; m⁴ - m² + 2m),C(√m; m⁴ - m² + 2m)

Do tính chất đối xứng, ta có ΔABC cân tại đỉnh A .

Vậy ΔABC đều chỉ cần

Kết hợp điều kiện ta có: m = ∛3 ( thỏa mãn).

Lưu ý: có thể sử dụng công thức b³/8a + 3 = 0 ⇔(-2m)³/8 + 3 = 0 ⇔ m³ = 3 ⇔ m = ∛3

Câu 7: Tìm tất cả các giá trị thực của tham số m để hàm số y = x³ - 3mx² + (m - 1)x + 2có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương.

A. 0 ≤ m ≤ 1.    B. m ≥ 1.    C. m ≥ 0.    D. m > 1.

Lời giải:

Đáp án : D

Giải thích :

Ta có y' = 3x² - 6mx + m - 1.

Hàm số có cực đại, cực tiểu khi và chỉ khi PT y' = 0 có hai nghiệm phân biệt

Điều này tương đương Δ' = 9m² - 3(m - 1) > 0 ⇔ 3m² - m + 1 > 0 (đúng với mọi m ).

Hai điểm cực trị có hoành độ dương

Vậy các giá trị cần tìm của m là m > 1.

Câu 8: Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x³ + 3mx + 1 có 2 điểm cực trị A,B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ ).

A. m = 3/2.    B. m = -1/2.    C. m = 1.     D. m = 1/2.

Lời giải:

Đáp án : D

Giải thích :

Ta có y' = -3x ² + 3m

y' = 0 ⇔ x² - m = 0(*)

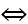
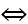
Đồ thị hàm số (1) có 2 điểm cực trị PT (*) có 2 nghiệm phân biệt m > 0(**)

Khi đó 2 điểm cực trị A(-√m; 1 - 2m√m) , B(√m; 1 + 2m√m)

Tam giác OAB vuông tại 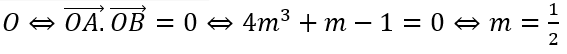( thỏa mãn).

Vậy m = 1/2.

Câu 9: Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x³ - 3(m + 1)x² + 12mx - 3m + 4(C) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm C(-1;-9/2) lập thành tam giác nhận gốc tọa độ O làm trọng tâm.

A. m = 1/2.    B. m = -2.     C. m = 2.    D. m = -1/2.

Lời giải:

Đáp án : D

Giải thích :

Ta có y' = 3x² - 6(m + 1)x + 12m. Hàm số có hai cực trị 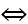y' = 0 có hai nghiệm phân biệt

⇔ (m - 1)² > 0 ⇔ m ≠ 1 (*). Khi đó hai điểm cực trị là A(2; 9m), B(2m; -4m³ + 12m² - 3m + 4).

Câu 10: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số

y = 2/3 x³ - mx² - 2(3m² - 1)x + 2/3 có hai điểm cực trị có hoành độ x₁ , x₂ sao cho

x₁ x₂ + 2(x₁ + x₂ ) = 1.

A.m = 0.    B.m = -2/3.     C. m = 2/3.    D.m = -1/2.

Lời giải:

Đáp án : C

Giải thích :

Ta có : y' = 2x² - 2mx - 2(3m² - 1) = 2(x² - mx - 3m² + 1),

g(x) = x² - mx - 3m² + 1 là tam thức bậc hai có Δ = 13m² - 4. Do đó hàm số có hai điểm cực trị khi và chỉ khi y' có hai nghiệm phân biệt g(x) có hai nghiệm phân biệt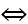

⇔ Δ > 0 ⇔ 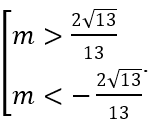(1)

x₁, x₂ là các nghiệm của g(x) nên theo định lý Vi-ét, ta có

Do đó x₁ x₂ + 2(x₁ + x₂ ) = 1 ⇔ -3m² + 2m + 1 = 1 ⇔ -3m² + 2m = 0 ⇔

Đối chiếu với điều kiện (1), ta thấy chỉ m = 2/3 thỏa mãn yêu cầu bài toán.

Câu 11: Gọi x₁, x₂ là hai điểm cực trị của hàm số y = x³ - 3mx² + 3(m² - 1)x - m³ + m . Tìm tất cả các giá trị của tham số thực m để : x₁² + x₂² - x₁ x₂ = 7

A. m = ±√2.    B. m = ±2.    C.m = 0.    D. m = ±1.

Lời giải:

Đáp án : B

Giải thích :

y' = 3x² - 6mx + 3(m² - 1)

Hàm số luôn luôn có cực trị với moi m

Theo định lí Viet :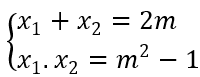

x₁² + x₂² - x₁ x₂ = 7 ⇔ (2m)² - 3(m² - 1) = 7 ⇔ m = ±2

Cách 2 : y’ = 0 ⇔ x² - 2mx + (m² - 1) = 0 ⇔

x₁² + x₂² - x₁ x₂ = 7 ⇔ (m + 1)² + (m - 1)² - (m - 1)(m + 1) = 7

⇔ m = ±2.

Câu 12: Cho hàm số y = x⁴ - 2(1 - m² )x² + m + 1 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất .

A. m = -1/2.    B. m = 1/2.     C. m = 0.    D. m =1.

Lời giải:

Đáp án : C

Giải thích :

[Phương pháp tự luận]

y' = 4x³ - 4(1 - m² )x

y' = 0 ⇔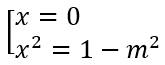

Hàm số có cực đại , cực tiểu khi và chỉ khi :|m| < 1

Tọa độ điểm cực trị A(0; m + 1)

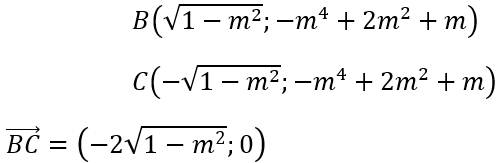
Phương trình đường thẳng BC : y + m⁴ - 2m² - m = 0

d(A, BC) = m⁴ - 2m² + 1 , BC = 2√(1 - m² )

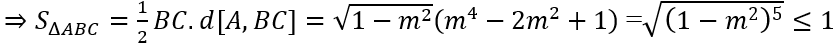
Vậy S đạt giá trị lớn nhất m = 0.

Khi đó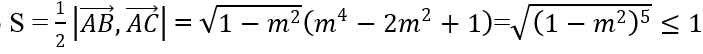

Vậy S đạt giá trị lớn nhất m = 0.