Biết rằng hàm số f(x)=căn x lnx đạt giá trị lớn nhất trên đoạn [1;e]

Câu hỏi:

Biết rằng hàm số $f (x) = \sqrt{x} \ln x$ đạt giá trị lớn nhất trên đoạn [1;e] tại $x = x_{0}$ . Mệnh đề nào sau đây đúng?

A. $x_{0} \in [1; \frac{3}{e}]$

B. $x_{0} \in (\frac{3}{e}; \sqrt{e})$

C. $x_{0} \in [\sqrt{e}; 2]$

D. $x_{0} \in (2; e]$

Trả lời:

Hàm số xác định và liên tục trên đoạn $[1; e]$

Đạo hàm

$f' (x) = (\sqrt{x})' . \ln x + \sqrt{x} (\ln x)' = \frac{\ln x}{2 \sqrt{x}} + \frac{1}{\sqrt{x}} = \frac{\ln x + 2}{2 \sqrt{x}}$

Suy ra

$f' (x) = 0 \Leftrightarrow \ln x + 2 = 0 \Leftrightarrow \ln x = - 2 \Leftrightarrow x = e^{- 2} = \frac{1}{e^{2}} \in [1; e]$

Ta có: $\{\begin{cases} f (1) = 0 \\ f (e) = \sqrt{e} \end{cases} \Rightarrow \underset{[1; e]}{m a x} f (x) = f (e) = \sqrt{e}$

Do đó $x_{0} = e$

Đáp án cần chọn là: D.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số $y = e^{- x} . \sin x$ . Mệnh đề nào sau đây đúng?

Xem lời giải »

Câu 2:

Cho giới hạn $I = \lim_{x \to \infty} \frac{e^{3 x} - e^{2 x}}{x}$ , chọn mệnh đề đúng:

Xem lời giải »

Câu 3:

Cho a, b là hai số thực thỏa mãn $a^{\frac{\sqrt{3}}{3}} > a^{\frac{\sqrt{2}}{2}}$ và $\log_{b} \frac{3}{4} < \log_{b} \frac{4}{5}$ . Mệnh đề nào sau đây là đúng?

Xem lời giải »

Câu 4:

Cho hàm số $f (x) = 2^{x} . 7^{x^{2}}$ . Khẳng định nào sau đây sai?

Xem lời giải »

Câu 5:

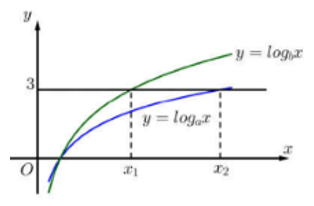
Hàm số $y = \log_{a} x$ và $y = \log_{b} x$ có đồ thị như hình vẽ bên:

Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ $x_{1}, x_{2}$ . Biết rằng $x_{2} = 2 x_{1}$ , giá trị của $\frac{a}{b}$ bằng

Xem lời giải »

Câu 6:

Tìm tất cả các giá trị thực của tham số m để hàm số: $y = \log_{3} (9^{x} - 3^{x} + m)$ có tập xác định là R.

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Biết rằng hàm số f(x)=căn x lnx đạt giá trị lớn nhất trên đoạn [1;e]

Xem thêm bài tập Toán có lời giải hay khác: