Các dạng bài tập về công thức lũy thừa, logarit và cách giải

---

Các dạng bài tập về công thức lũy thừa, logarit và cách giải

Với Các dạng bài tập về công thức lũy thừa, logarit và cách giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về công thức lũy thừa, logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

I. LÝ THUYẾT

a. Lũy thừa

+ Lũy thừa với số mũ nguyên

aⁿ = a.a....a, (n thừa số)

Ở đây n ∈ Z⁺, n > 1. Quy ước a¹ = a .

(a ≠ 0): a⁰ = 1, a^-n = 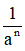với n ∈ Z⁺

+ Số căn bậc n

Với n lẻ và b ∈ R : Có một căn bậc n của b là ⁿ√b .

Với n chẵn

b < 0: Không tồn tại căn bậc n của b.

b = 0: Có một căn bậc n của b là 0.

b > 0: Có hai bậc n của b là ± ⁿ√b .

+ Tính chất căn bậc n

Giả thiết rằng mỗi biểu thức sau đều có nghĩa:

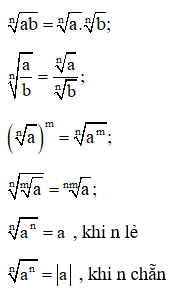
+ Lũy thừa số mũ hữu tỷ

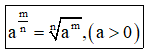
+ Lũy thừa số thực

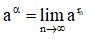(α là số vô tỉ, r_n là số hữu tỉ và lim r_n = α )

+ Tính chất

Giả thiết rằng mỗi biểu thức sau đều có nghĩa:

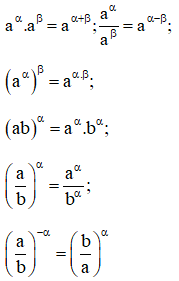
Nếu a > 1 thì a^α > a^β khi và chỉ khi α > β

Nếu a < 1 thì a^α > a^β khi và chỉ khi α < β

b. Logarit

+ Định nghĩa:

Cho 0 < a ≠ 1, b > 0.

Ta có: α = log_ab ⇔ a^α > b

- Lôgarit thập phân: log₁₀b = log b = lg b .

- Lôgarit tự nhiên: log_eb = ln b .

+ Các công thức:

Giả thiết rằng mỗi biểu thức sau đều có nghĩa:

log_aa = 1, log_a1 = 0

a^log_ab = b, log_a(a^α) = α

log_a(b₁.b₂) = log_ab₁ + log_ab₂

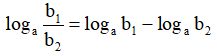
Đặc biệt : với a,b > 0, a ≠ 1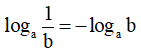

log_ab^α = αlog_ab

Đặc biệt: log_aⁿ√b =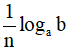

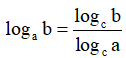
Đặc biệt: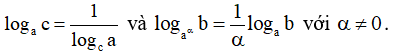

II. CÁC DẠNG BÀI VÀ PHƯƠNG PHÁP GIẢI

Dạng 1. Rút gọn biểu thức và tính giá trị của biểu thức

A. Phương pháp

Cách 1. Sử dụng định nghĩa và tính chất của lũy thừa và lôgarit

* Rút gọn biểu thức và tính biểu thức của lũy thừa.

+ Lũy thừa với số mũ nguyên

aⁿ = a.a....a, (n thừa số)

Ở đây n ∈ Z⁺, n > 1. Quy ước a¹ = a .

(a ≠ 0): a⁰ = 1, a^-n = 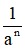với n ∈ Z⁺

+ Số căn bậc n

Với n lẻ và b ∈ R : Có một căn bậc n của b là ⁿ√b .

Với n chẵn

b < 0: Không tồn tại căn bậc n của b.

b = 0: Có một căn bậc n của b là 0.

b > 0: Có hai bậc n của b là ± ⁿ√b .

+ Tính chất căn bậc n

Giả thiết rằng mỗi biểu thức sau đều có nghĩa:

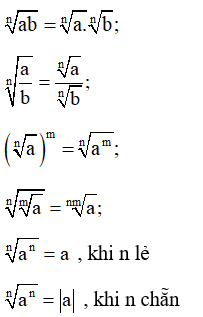
+ Lũy thừa số mũ hữu tỷ

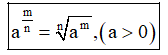
+ Lũy thừa số thực

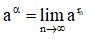(α là số vô tỉ, r_n là số hữu tỉ và lim r_n = α )

+ Tính chất

Giả thiết rằng mỗi biểu thức sau đều có nghĩa:

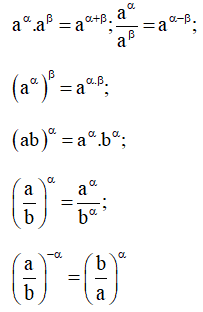
* Rút gọn biểu thức và tính biểu thức của logarit.

+ Định nghĩa:

Cho 0 < a ≠ 1, b > 0.

Ta có: α = log_ab ⇔ a^α > b

- Lôgarit thập phân: log₁₀b = log b = lg b .

- Lôgarit tự nhiên: log_eb = ln b .

+ Các công thức:

Giả thiết rằng mỗi biểu thức sau đều có nghĩa:

log_aa = 1, log_a1 = 0

a^log_ab = b, log_a(a^α) = α

log_a(b₁.b₂) = log_ab₁ + log_ab₂

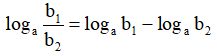
Đặc biệt : với a,b > 0, a ≠ 1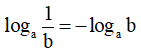

log_ab^α = αlog_ab

Đặc biệt: log_aⁿ√b =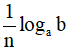

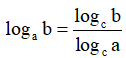
Đặc biệt: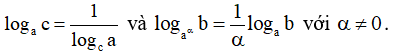

Cách 2. Sử dụng máy tính cầm tay.

B. Ví dụ minh họa

Câu 1. Cho là số thực dương. Giá trị của biểu thức 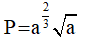bằng

Lời giải

Chọn D

Với a > 0, ta có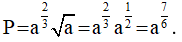

Câu 2. Rút gọn biểu thức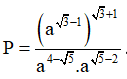

A. P = 2 . B. P = a² . C. P = 1 . D. P = a .

Lời giải

Chọn C

Ta có: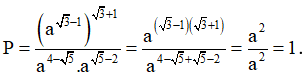

Cách 2: sử dụng máy tính cầm tay

Nhập vào máy tính:

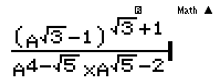
Sau đó bấm CALC thay một giá trị bất kì thỏa mãn a > 0 và a ≠ 1 và các đáp án phải khác nhau. Ta chọn A = 3. Khi đó ta có kết quả.

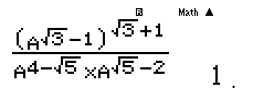
Câu 3. Với α là một số thực bất kỳ, mệnh đề nào sau đây sai?

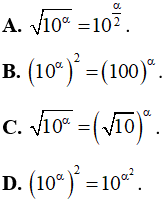
Lời giải

Chọn D

+) Có 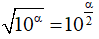với mọi α, nên A đúng.

+) Có (10^α)² = (100)^αvới mọi α , nên B đúng.

+) Có √10^α = (√10)^α với mọi α , nên C đúng.

+) Ta có (10^α)² = 10^2α ≠ 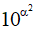. Do đó D sai.

Câu 4. Biểu thức 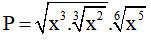(x > 0) viết dưới dạng lũy thừa với số mũ hữu tỷ là

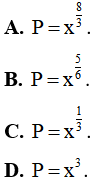
Lời giải

Chọn A

Ta có: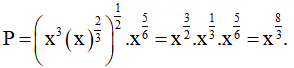

Câu 5. Tính giá trị biểu thức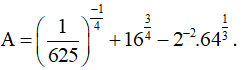

A. 14.

B. 12.

C. 11.

D. 10.

Lời giải

Chọn B

Ta có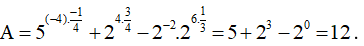

Câu 6. Cho a là số thực dương và a ≠ 1. Giá trị của biểu thức 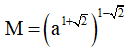bằng

Lời giải

Chọn D

Ta có: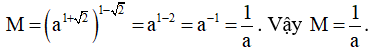

Câu 7. Cho a > 0, a ≠ 1 biểu thức 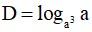có giá trị bằng bao nhiêu?

Lời giải

Chọn C

Ta có: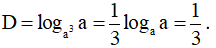

Câu 8. Với a và b là hai số thực dương, a ≠ 1. Giá trị của 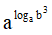bằng

Lời giải

Chọn D

Áp dụng công thức: a^log_ab = b

Ta có: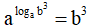

Câu 9. Tính giá trị của 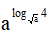với a > 0, a ≠ 1.

A. 16. B. 8 . C. 4 . D. 2 .

Lời giải

Chọn A

Ta có: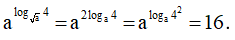

Câu 10. Cho a là số thực dương khác 4. Tính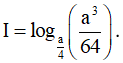

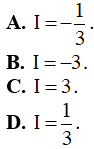
Lời giải

Chọn C

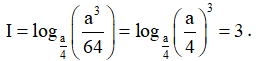
Câu 11. Trong các đẳng thức sau, đẳng thức nào sai?

A. ln(2e²) = 2 + ln2.

B. ln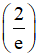 = ln 2 - 1.

C. ln √4e = 1 + ln 2 .

D. ln(e) = 1 .

Lời giải

Chọn C

ln √4e = ln√4 + ln √e = ln 2 +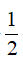

Câu 12. Tính giá trị của biểu thức: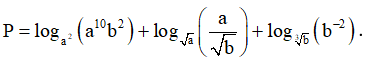

A. √3 . B. 1 . C. √2 . D. 2 .

Lời giải

Chọn B

Ta có:

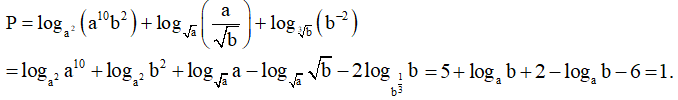
Dạng 2. So sánh các lũy thừa, logarit

A. Phương pháp giải.

Cách 1. Sử dụng tính chất của lũy thừa, lôgarit

a. So sánh các lũy thừa

Nếu a > 1 thì a^α > a^β khi và chỉ khi α > β

Nếu a < 1 thì a^α > a^β khi và chỉ khi α < β

b. So sánh các logarit

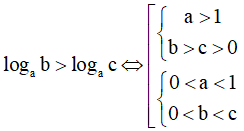
Cách 2. Sử dụng máy tính casio

B. Ví dụ minh họa

Câu 1. Cho a > 1. Mệnh đề nào sau đây là đúng?

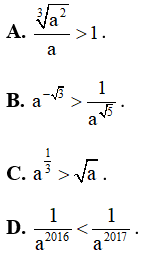
Lời giải

Chọn B

Vì cơ số a > 1 nên ta có a^m > aⁿ ⇔ m > n.

Xét phương án A: 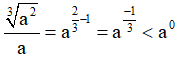=> phương án A sai.

Xét phương án B: 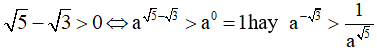=> hay phương án B đúng.

Xét phương án C: 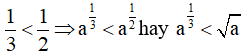=> phương án C sai.

Xét phương án C: 2016 < 2017 ⇔ a²⁰¹⁶ < a²⁰¹⁷ ⇔ 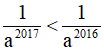=> phương án D sai.

Vậy phương án đúng là phương án B

Câu 2. Cho π^α > π^β với α,β ∈ R. Mệnh đề nào dưới đây là đúng?

A. α > β. B.α < β . C. α = β . D. α ≤ β .

Lời giải

Chọn A

Do π > 1 nên π^α > π^β ⇔ α > β .

Câu 3. Cho số thực a thỏa mãn a³ > a^π . Mệnh đề nào sau đây đúng?

A. 0 < a < 1 . B. a < 0 . C. a > 1 . D. a = 1 .

Lời giải

Chọn A

Ta có a³ > a^π mà 3 < π nên 0 < a < 1.

Câu 4. Mệnh đề nào dưới đây đúng?

Lời giải

Chọn C

Vì cơ số là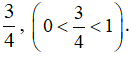

Do đó 5 < 6 nên 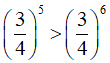là mệnh đề đúng.

Câu 5. Nếu 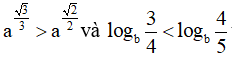thì

A. 0 < a < 1, 0 < b < 1 B. 0 < a < 1, b > 1

C. a > 1, b > 1 D. a > 1, 0 < b < 1

Lời giải

Chọn B

Ta có 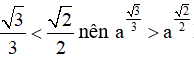khi 0 < a < 1

Ta lại có 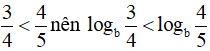khi b > 1

Vậy 0 < a < 1, b > 1

Câu 6. Chọn khẳng định sai trong các khẳng định sau:

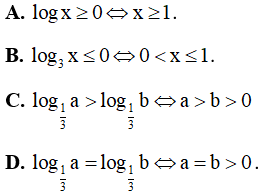
Lời giải

Chọn C

Ta có log x ≥ 0 ⇔ x ≤ 10⁰ nên x ≤ 1 là khẳng định đúng.

log₃^x ≤ 0 ⇔ 0 < x ≤ 3⁰ nên 0 < x ≤ 1 là khẳng định đúng.

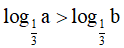⇔ b > a > 0 nên khẳng định C sai.

D đúng do tính đơn điệu của hàm số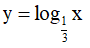

III. BÀI TẬP TỰ LUYỆN

Câu 1. Tính giá trị biểu thức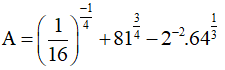

A. 15. B. 28. C. -11. D. 10.

Câu 2. Cho biểu thức 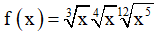. Khi đó giá trị của f(2,7) bằng:

A. 0,027 . B. 27 . C. 2,7 . D. 0,27 .

Câu 3. Tính giá trị của biểu thức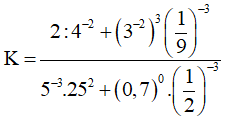

Câu 4. Trong các biểu thức sau, biểu thức nào không có nghĩa?

Câu 5. Với các số thực bất kỳ, mệnh đề nào dưới đây đúng?

Câu 6. Cho số thực x và số thực y ≠ 0 tuỳ ý. Mệnh đề nào dưới đây sai?

A. 3^x.3^y = 3^x+y.

B. (5^x)^y = (5^y)^x .

C.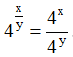

D. (2.7)^x = 2^x.7^x .

Câu 7. Cho a là số thực dương tùy ý và a khác 1, đặt 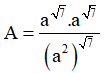. Mệnh đề nào sau đây đúng?

A. A = √7 . B. A = 1 . C. A = 2 . D.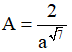

Câu 8. Cho a > 0 ; b > 0. Viết biểu thức 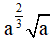về dạng a^m và biểu thức 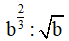về dạng bⁿ. Ta có m - n = ?

C. 1 . D. -1 .

Câu 9. Cho số thực a dương và m,n ∈ R. Mệnh đề nào sau đây đúng?

A. a^m+n = (a^m)ⁿ .

B. a^m+n = .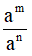

C. a^m+n = a^m.aⁿ

D. a^m+n = a^m + n

Câu 10. Cho số dương a và m,n ∈ R. Mệnh đề nào sau đây đúng?

A. a^m.aⁿ = a^m-n.

B. a^m.aⁿ =(a^m)ⁿ

C. a^m.aⁿ = a^m+n.

D. a^m.aⁿ = a^m.n.

Câu 11. Cho a là số dương tuỳ ý, ⁴√a³ bằng

Câu 12. Tính giá trị của biểu thức 2^log₂a + log_a(a^b) (a > 0, a ≠ 1).

A. P = a - b B. P = 2^a + b . C. P = a + b . D. P = 2a + b .

Câu 13. Cho a là số thực dương khác 1. Tính P = log_a√a .

A. P = 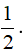. B. P = -2 . C. P = 2 . D. P = 0 .

Câu 14. Cho a,b > 0. Nếu lnx = 5lna + 2ln√b thì x bằng

A. a⁵ + b . B. a⁵b . C. 10a√b. D. .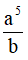

Câu 15. Với a là số thực dương tùy ý, log(8a) - log(3a) bằng

A. 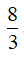. B. log₃⁸ . C. log 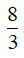. D. log(5a) .

Câu 16. Cho (√2 - 1)^m < (√2 - 1)ⁿ. Khi đó:

A. m > n. B. m < n. . C. m = n. . D. m ≤ n. .

Câu 17. Trong các khẳng định sau, khẳng định nào sai ?

A. log₃⁵ > 0 .

B. log _{2+ x²} 2016 < log _{2+ x²} 2017.

C. log_0,3^0,8 < 0 .

D.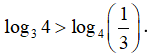

Câu 18. Mệnh đề nào dưới đây sai?

A. logx < 1 ⇔ 0 < x < 10.

B. lnx ≥ 0 ⇔ x ≥ 1.

C.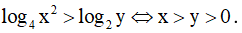

D.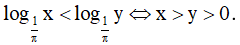

Đáp án:

1. B	2. C	3. D	4. B	5. A	6. C	7. B	8. C	9. C
10. C	11. C	12. C	13. A	14. B	15. C	16. A	17. C	18. C