Cách giải bài tập về Phép biến hình cực hay - Toán lớp 12

Cách giải bài tập về Phép biến hình cực hay

Với Cách giải bài tập về Phép biến hình cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về Phép biến hình từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

1. Phương pháp giải

+ Phép đối xứng qua mặt phẳng: Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó và biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của đoạn thẳng MM’.

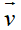
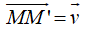
+ Phép tịnh tiến theo vecto là phép biến hình biến mỗi điểm M thành điểm M’ sao cho

+ Phép đối xứng qua đường thẳng: cho đường thẳng d, phép đối xứng trục qua đường thẳng d là phép biến hình biến mỗi điểm M thuộc d thành chính nó và biến mỗi điểm M không thuộc d thành điểm M’ sao cho trong mặt phẳng (M; d), d là đường trung trực của MM’.

+ Phép đối xứng tâm: Cho điểm O, phép đối xứng qua điểm O là phép biến hình biến mỗi điểm M thành điểm M’ sao cho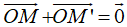

+ Phép vị tự: Cho số k không đổi khác 0 và một điểm O cố định. Phép biến hình trong không gian biến mỗi điểm M thành điểm M’ sao cho 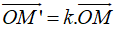gọi là phép vị tự. Điểm O gọi là tâm vị tự, số k được gọi là tỉ số vị tự

2. Ví dụ minh họa

Ví dụ 1. Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi

A. d song song với (P).

B. d nằm trên (P).

C. d vuông góc với (P) .

D. d nằm trên (P) hoặc d vuông góc với (P).

Hướng dẫn giải

Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi d nằm trên (P) hoặc (d)vuông góc với (P).

Chọn D.

Ví dụ 2. Trong không gian cho hai tam giác ABC và A'B'C' bằng nhau (AB = A'B'; AC = A'C'; BC = B'C'). Chọn mệnh đề đúng trong các mệnh đề sau

A. Không thể thực hiện một phép tịnh tiến nào biến tam giác này thành tam giác kia.

B. Tồn tại duy nhất một phép tịnh tiến nào biến tam giác này thành tam giác kia.

C. Có nhiều nhất hai phép tịnh tiến nào biến tam giác này thành tam giác kia.

D. Có thể thực hiện vô số phép tịnh tiến biến tam giác này thành tam giác kia.

Hướng dẫn giải

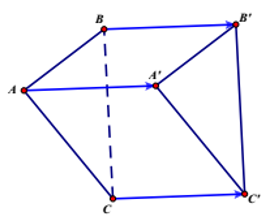
Trước hết ta nhận thấy rằng, muốn thực hiện được một phép tịnh tiến biến ΔABC thành ΔA'B'C' thì phải có điều kiện, hai tam giác ABC và A'B'C' phải nằm trên hai mặt phẳng song song (hoặc trùng nhau) và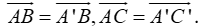

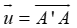
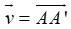
Khi đó phép tịnh tiến theo vecto biến ΔA'B'C' thành ΔABC và phép tịnh tiến theo vecto biến ΔABC thành ΔA’B’C’.

Như vậy chỉ có hai phép tịnh tiến biến tam giác này thành tam giác kia.

Chọn C.

Ví dụ 3. Cho hình lập phương ABCD. A'B'C'D'. Gọi I, J lần luợt là trung điểm của các cạnh AD, BC. Phép tịnh tiến theo vecto 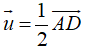biến tam giác A'IJ thành tam giác

A. C'CD.

B. CD'P với P là trung điểm của B'C'.

C. KDC với K là trung điểm của A’D’

D. DC'D'

Hướng dẫn giải

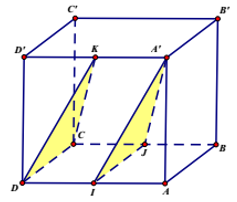
Gọi T là phép tịnh tiến theo vecto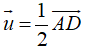

Ta có

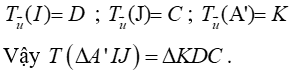
Chọn C.

Ví dụ 4. Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?

A. 1 mặt phẳng.

B. 4 mặt phẳng.

C. 7 mặt phẳng.

D. Có vô số mặt phẳng.

Hướng dẫn giải

Có 2 loại mặt phẳng thỏa mãn đề bài là:

* Loại 1: Mặt phẳng qua trung điểm của 3 cạnh bên có chung đỉnh. Có 4 mặt phẳng thỏa mãn loại này (vì có 4 đỉnh)

Nhận xét. Loại này ta thấy có 1 điểm nằm khác phía với 3 điểm còn lại.

* Loại 2: Mặt phẳng qua trung điểm của 4 cạnh ( 4 cạnh này thuộc 2 cặp cạnh, mỗi cặp cạnh là chéo nhau). Có 3 mặt phẳng như thế.

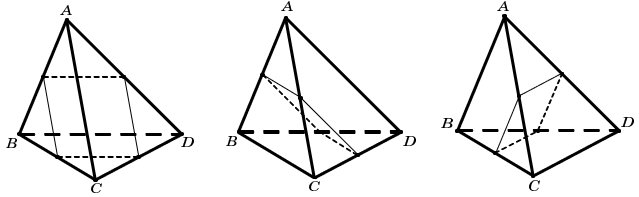
Nhận xét. Loại này ta thấy có 2 điểm nằm khác phía với 2 điểm còn lại.

Chọn C.

Ví dụ 5. Cho phép vị tự tâm O biến điểm A thành điểm B, biết rằng OA = 2O

B. Khi đó, tỉ số vị tự là bao nhiêu?

A. 2.

B. -2.

C.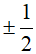

D. 1/2

Hướng dẫn giải

Theo giả thiết OA = 2OB nên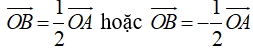

Vậy có hai phép vị tự 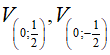biến điểm A thành điểm B.

Chọn C.