Dạng bài Tính chất đối xứng của khối đa diện cực hay - Toán lớp 12
Dạng bài Tính chất đối xứng của khối đa diện cực hay
Với Dạng bài Tính chất đối xứng của khối đa diện cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính chất đối xứng của khối đa diện từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
1. Phương pháp giải
Quy tắc tìm các mặt phẳng đối xứng:
Do tính chất đối xứng nhau, nên cứ đi từ trung điểm các cạnh ra mà tìm. Đảm bảo rằng nếu chọn 1 mặt phẳng đối xứng nào thì các điểm còn lại phải chia đều về 2 phía.
2. Ví dụ minh họa
Ví dụ 1. Số mặt phẳng đối xứng của hình tứ diện đều là:
A. 10.
B. 8.
C. 6.
D. 4.
Hướng dẫn giải
Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện.
Vậy hình tứ diện đều có 6 mặt phẳng đối xứng.
Chọn C
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có mặt đối xứng nào?
A. Không có.
B. (SAB).
C. (SAC).
D. (SAD)
Hướng dẫn giải
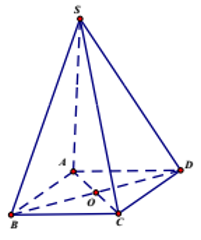
Ta có:
và O là trung điểm của BD. Suy ra (SAC) là mặt phẳng trung trực của BD.
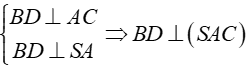
Suy ra (SAC) là mặt đối xứng của hình chóp, và đây là mặt phẳng duy nhất.
Chọn C.
Ví dụ 3. Gọi n1, n2, n3 lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?
A. n1= 0; n2 = 0; n3 = 6
B. n1 = 0; n2 = 1; n3 = 9
C. n1 = 3; n2 = 1; n3 = 9
D. n1 =0; n2= 1; n3 = 3
Hướng dẫn giải
+Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện).
+Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác).
+Khối lập phương có 9 trục đối xứng (Loại 1: đi qua tâm của các mặt đối diện ; Loại 2: đi qua trung điểm các cặp cạnh đối diện).
Chọn C.
Ví dụ 4. Trung điểm các cạnh của một tứ diện đều là
A. Các đỉnh của một hình tứ diện đều.
B. Các đỉnh của một hình bát diện đều.
C. Các đỉnh của một hình mười hai mặt đều.
D. Các đỉnh của một hình hai mươi mặt đều.
Hướng dẫn giải
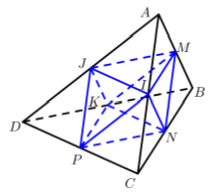
Ta chứng minh trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình bát diện đều.
+ Cho tứ diện đều ABCD cạnh a.
Gọi M, N, P, I, J, K lần lượt là trung điểm của các cạnh AB, BC, CD, AC, AD, DB.
+ Ta có: IM=IN=MN=1/2a (tính chất đường trung bình của tam giác).
Suy ra tam giác IMN đều.
+ Chứng minh tương tự, ta có các tam giác IPN, IPJ, KPJ, KPN, IMJ, KMJ, KMN là các tam giác đều.
+ Tám tam giác trên tạo thành một đa diện có các đỉnh là M, N, P, I, J, K mà mỗi đỉnh là đỉnh chung của đúng tam giác đều. Do đó đa diện đó là đa diện đều loại {3; 4} tức là bát diện đều.
Chọn B
Ví dụ 5. Chọn khẳng định đúng trong các khẳng định sau:
A. Tâm tất cả các mặt của 1 hình lập phương thì tạo thành một hình lập phương.
B. Tâm tất cả các mặt của 1 hình tứ diện đều thì tạo thành một hình tứ diện đều.
C. Tâm tất cả các mặt của 1 hình tứ diện đều thì tạo thành một hình lập phương.
D. Tâm tất cả các mặt của 1 hình lập phương thì tạo thành một hình tứ diện đều.
Hướng dẫn giải
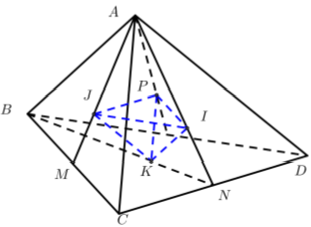
Gọi P, I, J, K là tâm của các mặt ABD, ACD, ABC, BCD của tứ diện đều ABCD.
+ Ta có: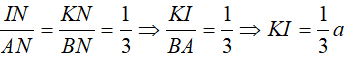 
+ Chứng minh tương tự ta có:
\
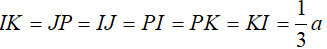
Vậy tứ diện PIJK là tứ diện đều.
Chọn B.
