Cách nhận dạng các khối đa diện cực hay - Toán lớp 12

Cách nhận dạng các khối đa diện cực hay

Với Cách nhận dạng các khối đa diện cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập nhận dạng các khối đa diện từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

* Cho hình (H) thỏa mãn hai đặc điểm :

+ Gồm một số hữu hạn đa giác phẳng

+ Phân chia không gian ra thành hai phần : phần bên trong và phần bên ngoài của hình đó.

Hình (H) cùng với các điểm nằm trong (H) được gọi là khối đa diện giới hạn bởi hình (H).

* Hình đa diện :

Xét các khối đa diện giới hạn bởi hình (H) gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện :

+ Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung, hoặc có 1 cạnh chung.

+Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác

Hình (H) gồm các đa giác như thế được gọi là một hình đa diện ( đa diện).

2. Ví dụ minh họa

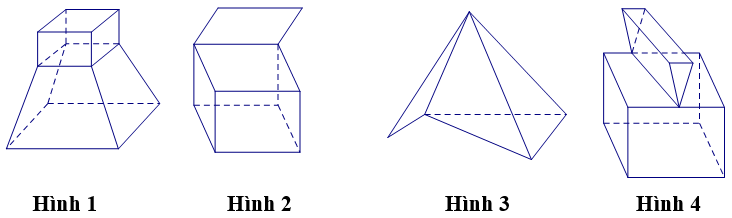
Ví dụ 1. Cho các hình sau:

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Hướng dẫn giải

Hình đa diện là hình tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:

1. Hai đa giác bất kì hoặc không có điểm chung hoặc chỉ có một đỉnh chung hoặc chỉ có một cạnh chung.

2. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Các hình 2, 3, 4 đều không thỏa mãn tính chất số 2.

Chọn A

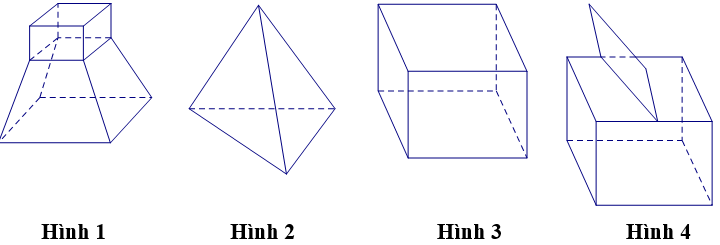
Ví dụ 2. Cho các hình sau:

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là: Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là:

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Hướng dẫn giải

Áp dụng các tính chất của hình đa diện:

+ Mỗi cạnh là cạnh chung bất kì của đúng hai mặt;

+ Hai mặt bất kì hoặc có 1 đỉnh chung, hoặc 1 cạnh chung, hoặc không có điểm chung nào.

Hình 4 không có tính chất 2: hai mặt bất kì có 1 điểm chung – nhưng điểm đó không phải là đỉnh.

Chọn D.

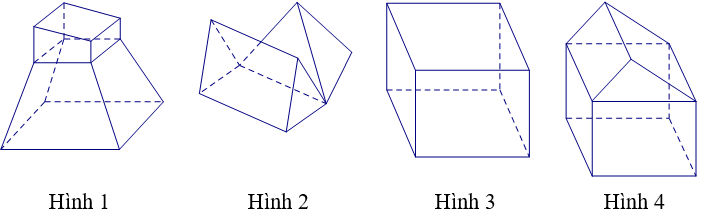
Ví dụ 3. Cho các hình sau:

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là:

A. 1.

B. 2.

C. 3.

D. 4.

Hướng dẫn giải

Các hình 1; hình 3; hình 4 là các hình hữu hạn đa giác phẳng thỏa mãn 2 điều kiện:

+ Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung hoặc có 1 cạnh chung

+ Mỗi cạnh của 1 đa giác là cạnh chung của đúng 2 đa giác.

Do đó, các hình 1, 3 và hình 4 là các hình đa diện.

Chọn C.

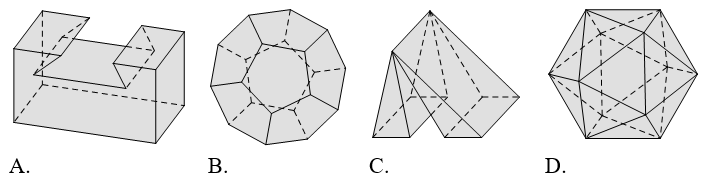
Ví dụ 4. Vật thể nào trong các vật thể sau không phải là hình đa diện?

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

A. Hình A

B. Hình B

C.Hình C

D. Hình

D.

Hướng dẫn giải

Hình C không thỏa mãn điều kiện: “Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác”. Do đó, hình C không phải là hình đa diện.

Chọn C.

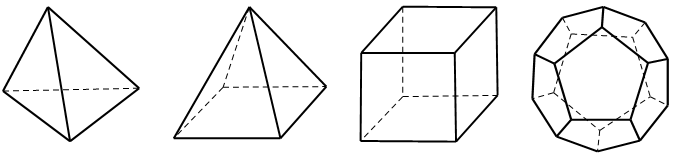
Ví dụ 5. Khối đa diện nào sau đây có số mặt nhỏ nhất?

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

A. Khối tứ diện đều

B. Khối chóp tứ giác

C. Khối lập phương

D.Khối 12 mặt đều

Hướng dẫn giải

+ Khối tứ diện đều có bốn mặt.

+ Khối chóp tứ giác có năm mặt.

+ Khối lập phương có sáu mặt.

+ Khối 12 mặt đều có 12 mặt

Do đó, khối tứ diện đều có số mặt nhỏ nhất.

Chọn A.