Dạng bài Tính chất của khối đa diện cực hay - Toán lớp 12

Dạng bài Tính chất của khối đa diện cực hay

Với Dạng bài Tính chất của khối đa diện cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính chất của khối đa diện từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Gọi m, c, d theo thứ tự là số mặt, số cạnh, số đỉnh của đa diện (H)

• Ta luôn có: m,d≥4; c≥6 ; m < c; d < c (1)

• Nếu mỗi đa diện (H) có chung p cạnh thì

         mp = 2c (2)

• Nếu mỗi đỉnh của đa diện là đỉnh chung của p mặt thì ta có

         dq = 2c (3)

• Công thức Ơ-le: d + m – c= 2 (4)

2. Ví dụ minh họa

Ví dụ 1. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Mỗi hình đa diện có ít nhất bốn đỉnh.

B. Mỗi hình đa diện có ít nhất ba cạnh.

C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.

D. Số mặt cảu một hình đa diện lớn hơn hoặc bằng số cạnh của nó.

Hướng dẫn giải

- A Đúng: Ta chứng minh như sau:

Gọi M₁ là môt mặt khối đa diện, M₁ là đa giác nên có ít nhất 3 cạnh c₁; c₂; c₃.

M₂ chung cạnh c₁ với M₁(M₂≠M₁) , M₃ chung cạnh c₂ với M₁(M₃≠M₁)

Vì c₁∈M₃⇒M₂≠M₃. Gọi M₄ là mặt có chung cạnh c₃ với M₁(M₄≠M₁)

Vì M₄ không chứa c₁, c₂ nên M₄ khác M₂ và M₃. Do đó khối đa diện có ít nhất 4 mặt ⇒ mỗi hình đa giác có ít nhất 4 đỉnh.

- B Sai.

- C Sai: Ví dụ như hình chóp tam giác có 4 đỉnh nhưng có 6 cạnh.

- D Sai: Lấy ví dụ là hình chóp tam giác có 4 mặt nhưng có 6 cạnh.

Chọn A.

Ví dụ 2. Một hình chóp có 46 cạnh có bao nhiêu mặt?

A.24

B.46

C.69

D.25

Hướng dẫn giải

Giả sử đa giác đáy có n cạnh.

Suy ra hình chóp có 2n cạnh.

Theo giả thiết giả thiết hình chóp có 46 cạnh nên ta có: 2n = 46

⇔ n= 23.

Do đó, có 23 mặt bên và 1 mặt đáy. Do đó hình chóp có tổng cộng là 24 mặt.

Chọn A

Ví dụ 3. Phát biểu nào sau đây là đúng?

A. Hình hai mươi mặt đều có 30 đỉnh, 12 cạnh, 20 mặt.

B. Hình hai mươi mặt đều có 20 đỉnh, 30 cạnh, 12 mặt.

C. Hình hai mươi mặt đều có 12 đỉnh, 30 cạnh, 20 mặt

D. Hình hai mươi mặt đều có 30 đỉnh, 20 cạnh, 12 mặt.

Hướng dẫn giải

Khối 20 mặt đều có các mặt là tam giác đều, mỗi đỉnh là đỉnh chung của 5 cạnh

Gọi số đỉnh là n. Suy ra, số cạnh là 5n/2

Theo định lí Ơ-le: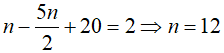

Vậy số đỉnh là 12, số cạnh là 30.

Chọn C

Ví dụ 4. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Số đỉnh và số mặt của mọi hình đa diện luôn luôn bằng nhau.

B. Số đỉnh của mọi hình đa diện luôn lớn hơn 4.

C. Tồn tại một hình đa diện có số cạnh gấp hai lần số đỉnh.

D. Tồn tại một hình đa diện có số cạnh nhỏ hơn 6.

Hướng dẫn giải

- Hình lập phương có 8 đỉnh, 6 mặt. Số đỉnh khác số mặt. Vậy loại A.

- Hình tứ diện có 4 đỉnh, suy ra số đỉnh của hình đa diện có thể không lớn hơn 4. Vậy loại B

- Hình tứ diện là hình có số cạnh ít nhất (bằng 6). Do đó không tồn tại hình đa diện có số cạnh nhỏ hơn 6. Vậy loại D

- Hình bát diện có số cạnh gấp hai lần số đỉnh.

Chọn C.

Ví dụ 5. Một hình đa diện có các mặt là những tam giác thì số mặt M và số cạnh C của đa diện đó thoả mãn

A. 3C= 2M.

B. C= M+ 2.

C. M≥C

D. 3M= 2C

Hướng dẫn giải

- Mỗi mặt có 3 cạnh.

- Mỗi cạnh lại là cạnh chung của đúng hai mặt.

- Do đó số cạnh là: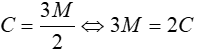

Chọn D.

Ví dụ 6. Biết rằng khối đa diện mà mỗi mặt đều là hình tam giác. Gọi n là số mặt của khối đa diện đó, lúc đó ta có

A. n là số chia hết cho 3.

B. n là số chẵn.

C. n là số lẻ.

D. n là số chia hết cho 5 .

Hướng dẫn giải

Gọi số cạnh và số mặt của khối đa diện lần lượt là c và n.

Vì mỗi mặt có ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt nên ta có số cạnh của đa diện là c=3n/2

Suy ra 3n= 2c => 3n là số chẵn ⇒ n là số chẵn.

Chọn B.