Cho đoạn thẳng AB và hai tia Ax, By vuông góc với AB ở trên cùng một nửa mặt phẳng bờ AB. Gọi O là trung điểm của AB.

Cho đoạn thẳng AB và hai tia Ax, By vuông góc với AB ở trên cùng một nửa mặt phẳng bờ AB. Gọi O là trung điểm của AB. Xét góc vuông $\widehat{mOn}$ quay quanh O sao cho Om cắt Ax tại C, On cắt By tại D. Chứng minh rằng:

a) CD luôn tiếp xúc với nửa đường tròn $\left(O;\frac{AB}{2}\right)$

b) $AC.BD=\frac{A{B}^2}{4}$

Xét góc vuông $\widehat{mOn}$ quay quanh O sao cho Om cắt Ax tại C, On cắt By tại D nên $\widehat{COD}=90°$

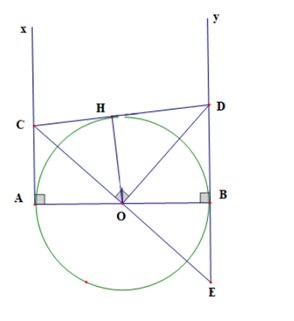
a) Kẻ OH ⊥ CD

Ta có DC = DE (chứng minh câu a)

Suy ra tam giác DCE cân ở D

Mà DO là đường cao nên DO đồng thời là phân giác của $\widehat{CDE}$

Suy ra $\widehat{CDE}=\widehat{CDO}$

Xét ∆HOD và ∆BOD có

$\widehat{DHO}=\widehat{DBO}=90°$

OD là cạnh chung

$\widehat{H}=\widehat{ODB}$

Suy ra ∆HOD = ∆BOD (cạnh huyền – góc nhọn)

Do đó OH = OB, HD = BD (các cặp cạnh tương ứng)

Mà OB là bán kính của (O)

Suy ra H thuộc (O)

Lại có OH ⊥ CD nên CD là tiếp tuyến của (O)

c)  Xét ∆HOC và ∆AOC có

OH = OA (= OB)

$\widehat{CHO}=\widehat{CAO}=90°$

OC là cạnh chung

Suy ra ∆HOC = ∆AOC (cạnh huyền – cạnh góc vuông)

Do đó HC = AC

Xét tam giác COD vuông tại O có OH ⊥ CD

Theo hệ thức lượng trong tam giác có

OH² = CH . DH

Ta có: $AC.BD=CH.DH=O{H}^2=O{A}^2={\left(\frac{BC}{2}\right)}^2=\frac{B{C}^2}{4}$

Vậy $AC.BD=\frac{A{B}^2}{4}$