Cho đường tròn (O, 13cm) và dây AB = 24cm. Trên các tia OA
Câu hỏi:
Cho đường tròn (O, 13cm) và dây AB = 24cm. Trên các tia OA, OB lần lượt lấy M, N sao cho OM = ON = 33,8cm. Chứng minh MN là tiếp tuyến của (O).
Trả lời:
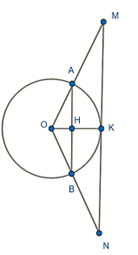
Gọi K là giao điểm OH và MN; Gọi H là giao của OK và AB
Ta có: OA = OB nên OAB cân tại O ⇒ H là trung điểm của AB.
Có OM = ON; OA = OB = R
Nên: \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}}\). Suy ra: AB // MN (định lý Thales đảo)
⇒ HA = HB = 12cm
Xét ΔOKN có BH // KN
Nên: \(\frac{{BH}}{{KN}} = \frac{{OB}}{{ON}}\)
⇒ KN = 31,2cm
⇒ OK = \(\sqrt {33,{8^2} - 31,{2^2}} = 13\left( {cm} \right)\) = R
Suy ra: K thuộc (O)
Ta có: OK ⊥ MN và OK là bán kính của (O)
Vậy MN là tiếp tuyến của (O).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Xét xem dãy un = 3n – 1 có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.
Xem lời giải »
Câu 2:
Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2018, số lượng người xem phim tăng lên 45% nên tổng doanh thu cũng tăng 8,75%. Hỏi rạp phim đã giảm giá mỗi vé bao nhiêu % so với giá bán ban đầu?
Xem lời giải »
Câu 3:
Tính giá trị của biểu thức: P = (x – 10)2 – x(x + 80) tại x = 0,87.
Xem lời giải »
Câu 4:
Tính giá trị biểu thức A = 100 – 99 + 98 – 97 + … + 4 – 3 + 2.
Xem lời giải »
Câu 5:
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g(x) = \(\frac{1}{{f\left( x \right) - 1}}\) là?
Xem lời giải »
Câu 6:
Chứng minh rằng biểu thức sau luôn dương với mọi x.
a) 9x2 – 6x + 2;
b) x2 + x + 1;
c) 2x2 + 2x + 1.
Xem lời giải »
Câu 7:
Tìm số nguyên tố p để p + 2, p + 6 và p + 8 đều là số nguyên tố.
Xem lời giải »



