Tìm số tự nhiên n sao cho 2n + 3 chia hết cho n – 2.
Câu hỏi:
Tìm số tự nhiên n sao cho 2n + 3 chia hết cho n – 2.
Trả lời:
Ta có: 2n + 3 = 2(n – 2) + 7
Vì 2(n – 2) chia hết cho n – 2 nên để 2n + 3 chia hết cho n – 2 thì 7 chia hết cho (n – 2)
Hay (n – 2) ∈ Ư(7)
⇒ n – 2 ∈ {1;7} (vì n là số tự nhiên)
⇒ n ∈ {3; 9}
Vậy n = 3 hoặc n = 9.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Chứng minh rằng A = 1.5 + 2.6 + 3.7 + … + 2023.2027 chia hết cho 11, 23 và 2023.
Xem lời giải »
Câu 4:
Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD
a) Chứng minh rằng AF // CE.
b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.
Xem lời giải »
Câu 5:
Cho . Tính giá trị biểu thức A = tanα + cotα.
Xem lời giải »
Câu 6:
Cho biết a // b và góc = 120°.
a) Tính góc .
b) So sánh góc và góc .
c) Tính
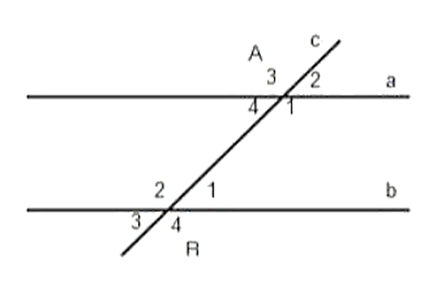
Xem lời giải »
Câu 7:
Cho tam giác ABC cân tại A lấy điểm D bất kì trên AB, lấy điểm E trên tia đối của tia CA sao cho CE = BD. Từ D kẻ đường thẳng song song với AC cắt BC tại F
a) Tam giác DBF là tam giác gì?
b) Chứng minh tứ giác DCEF là hình bình hành.
Xem lời giải »
Câu 8:
Chứng minh 3n + 11 và 3n + 2 là hai số nguyên tố cùng nhau với mọi số tự nhiên n.
Xem lời giải »


