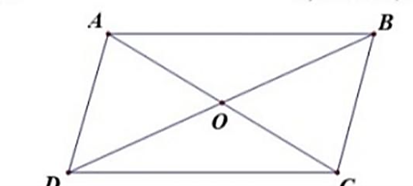
Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.

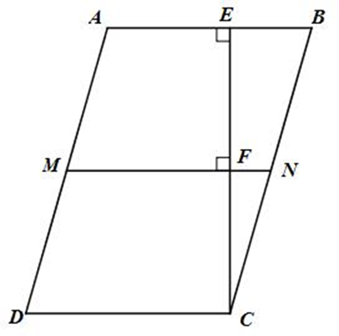
a) Ta có MN ⊥ CE (gt); AB ⊥ CE (gt)

Suy ra: MN // AB

Mà AB // CD (ABCD là hình bình hành) nên MN // CD

Tứ giác MNCD có MN // CD

Và MD // CN (AD // BC)

Do đó tứ giác MNCD là hình bình hành.

b) Gọi F là giao điểm của MN và EC

Hình thang AECD (EC // CD) có MF // AE // CD

Và M là trung điểm của AD (gt)

*  F là trung điểm của EC.

ΔMEC có MF là đường trung tuyến (F là trung điểm của EC)

Và MF là đường cao

Suy ra:  ΔMEC cân tại M.

c) Ta có AD = 2AB (gt)

AD = 2MD (M là trung điểm của AD)

Và AB = CD (ABCD là hình bình hành); MD = CD

Hình bình hành MNCD có MD = CD nên là hình thoi.

CM là đường phân giác nên: $\widehat{EMF}=\widehat{CMF}$

Mà $\widehat{EMF}=\widehat{AEM}$ (hai góc so le trong và AE // MF)

Và $\widehat{CMF}=\widehat{MCD}$ (hai góc so le trong và MF // CD)

Nên: $\widehat{MCD}=\widehat{AEM}$

Ta có: $\widehat{MCD}=\widehat{AEM}; 2\widehat{MCD}=\widehat{NCD}$ (CM là phân giác $\widehat{NCD}$)

Và $\widehat{BAD}=\widehat{NCD}$ (ABCD là hình bình hành)

Vậy $\widehat{BAD}=2\widehat{AEM}$.