Cho (O; R) đường kính AB và M nằm trên (O; R) với MA < MB (M khác A và B). Tiếp tuyến tại M của (O; R) cắt tiếp tuyến tại A và B của (O; R) theo thứ tự ở C và D.

a) Chứng minh ACDB là hình thang vuông

b) AD cắt (O; R) tại E, OD cắt MB tại N. Chứng minh OD vuông góc MB và DE.DA = DN.DO

c) Cho AM = R. Tính theo R diện tích ACDB.

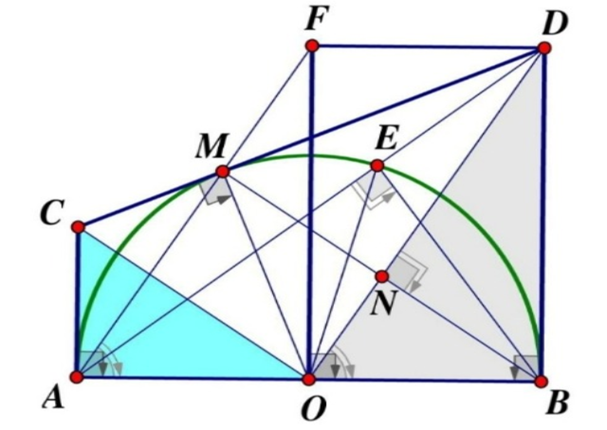
a) AC ⊥ AB vì AC là tiếp tuyến

BD ⊥ AB vì BD là tiếp tuyến

Suy ra: AC // DB ⇒ ACDB là hình thang

Lại có: $\widehat{BAC}=\widehat{DBA}=90°$ nên ACDB là hình thang vuông

b) Theo tính chất 2 tiếp tuyến cắt nhau

Ta có: MD = MB

OM = OB = R

Nên OD là đường trung trực của MB

⇒ OD ⊥ MB và MN = NB

Xét tam giác OBD vuông tại B có OD ⊥ BN

Áp dụng hệ thức lượng trong tam giác vuông: DN.DO = BD² (1)

Tam giác AEB có OE = OA = OB = R nên tam giác AEB vuông tại E

Suy ra: BE ⊥ DA

Lại có: tam giác ABD vuông tại B và OD ⊥ BE

 ⇒ DE.DA = BD² (2)

Từ (1) và (2) suy ra: DE.DA = DN.DO

c) Ta có: MA = OA = OM = R nên tam giác AMO đều

⇒ $\widehat{AOM}=60°\Rightarrow \widehat{AOC}=30°$ (vì OC là phân giác)

⇒ $\widehat{BOM}=120°\Rightarrow \widehat{BOD}=60°$

Xét trong tam giác BOD có: $BD=OB.\tan 60°=R\sqrt{3}$

Trong tam giác OCA có: $AC=OA.\tan 30°=\frac{R\sqrt{3}}{3}$

Vì ACDB là hình thang vuông AB là đường cao

Nên $S_{ACDB}=\frac{1}{2}.AB.\left(AC+BD\right)=\frac{4R^2\sqrt{3}}{3}$