Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.
a) Tính HB, HC.
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AB.AC = EF.BC.
Trả lời:
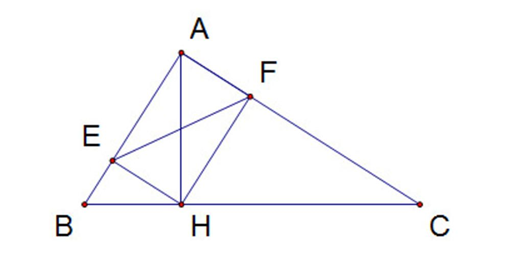
a) Xét ΔABH và ΔCBA có:
chung
⇒ ΔABH ∽ ΔCBA(g.g)
⇒
Hay
Xét ΔABC vuông tại A, đường cao AH có:
AB2 = HB.BC ( hệ thức lượng trong Δ vuông )
⇔ 152 = HB.25
⇔ 225 = HB.25
⇔ HB = 9 (cm)
HB + HC = BC
⇔ 9 + HC = 25
⇔ HC = 16(cm)
b) Xét tứ giác AEHF có:
Nên AEHF là hình chữ nhật
⇒ AH = EF
Xét ΔABC vuông tại A, đường cao AH có:
AB.AC = AH.BC (hệ thức lượng trong Δ vuông)
⇒ AB.AC = EF.BC (vì AH = EF).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính
Xem lời giải »
Câu 2:
Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, . Bán kính đường tròn nội tiếp tam giác ABC là cm. Tính đường cao AH của tam giác ABC.
Xem lời giải »
Câu 3:
Cho C = 5 + 52 + … + 520. Chứng minh rằng C chia hết cho 5, 6, 13.
Xem lời giải »
Câu 5:
Cho tam giác đều ABC. Gọi M là điểm thuộc cạnh BC. Gọi E, F lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC. Gọi I là trung điểm của AM, D là trung điểm của BC.
a, Tính góc DIE và góc DIF.
b, Chứng minh rằng: tứ giác DEIF là hình thoi.
Xem lời giải »
Câu 6:
Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.
Xem lời giải »
Câu 7:
Tìm x sao cho: (x + 5)(4 − 3x) − (3x + 2)2 + (2x + 1)3 = (2x − 1)(4x2 + 2x + 1).
Xem lời giải »


