Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và

Câu hỏi:

Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và 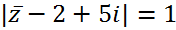. Hỏi có bao nhiêu số phức z thỏa mãn

A. 1

B. 2

C. 3

D. 4

Trả lời:

Chọn B.

Gọi số phức cần tìm là z = a + bi.

Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)

= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i

+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a

+ ta có 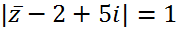⇔|a – 2 + (-b + 5)i| = 1

Hay ( a - 2) ²+ ( 5 - 3a) ²= 1

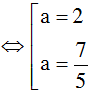(thỏa mãn)

Vậy có hai số phức z thỏa mãn là z = 2 + 6i và $z = \frac{7}{5} + \frac{21}{5} i$

Câu 1:

Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.

Câu 2:

Cho số phức z thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z là?

Câu 3:

Tìm nghiệm của phương trình:

Câu 4:

Tìm nghiệm của phương trình: ( z + 3 - i)²- 6( z + 3 - i) + 13 = 0

Câu 5:

Tìm số phức z biết |iz + 1 | = $\sqrt{2}$ và ( 1 + i) z + 1 – 2i là số thuần ảo.

Câu 6:

Biết z₁; z₂ là hai số phức thỏa điều kiện: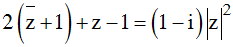 . Tính z₁+ z₂

Câu 7:

Biết z₁; z₂ là số phức thỏa mãn:.

Tính

Các dạng bài tập Toán lớp 12