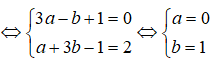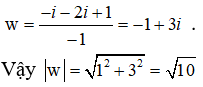Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: w = z ngang
Câu hỏi:
Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: là
A. 2
B. 4
C.
D. 10
Trả lời:
Đặt z = a + bi(a, b ∈ R). Ta có :
(1 + i)(z - i) = (1 + i)[a + (b - 1)i] = a - b + 1 + (a + b - 1)i
Từ giả thiết ta có: (1 + i)(z - 1) + 2z = 2i
⇔ a - b + 1 + (a + b - 1)i + 2(a + bi) = 2i ⇔ (3a - b + 1) + (a + 3b - 1)i = 2i
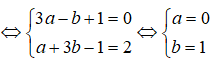
Suy ra z = i và
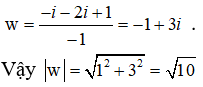
Chọn C
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hai số phức Phần thực và phần ảo của số phức là
Xem lời giải »
Câu 2:
Phần thực và phần ảo của số phức là
Xem lời giải »
Câu 4:
Thực hiện phép tính: ta có
Xem lời giải »
Câu 5:
Cho số phức z thỏa mãn Khi đó môđun của số phức là
Xem lời giải »
Câu 7:
Phương trình có 4 nghiệm phức Giá trị biểu thức bằng
Xem lời giải »
Câu 8:
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z - 2i| = 4 là
Xem lời giải »