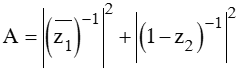Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| nhỏ hơn bằng 2
Câu hỏi:
Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích
A. S = 9π.
B. S = 12π.
C. S = 16π.
D. S = 25π.
Trả lời:
Chọn C.
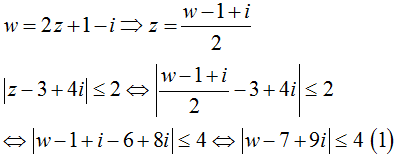
Giả sử w = x + yi , khi đó ( 1) tương đương ( x - 7) 2+ ( y + 9) 2 ≤ 16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4
Vậy diện tích cần tìm là S = π.42 = 16π.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
Xem lời giải »
Câu 2:
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
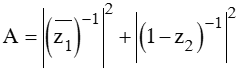
Xem lời giải »
Câu 3:
Gọi z1; z2 lần lượt là hai nghiệm của phương trình z2 – 4z + 7 = 0 .Tính giá trị của biểu thức 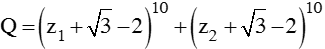
Xem lời giải »
Câu 4:
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
Xem lời giải »
Câu 5:
Trong mặt phẳng phức Oxy, tâp hợp các điểm biểu diễn số phức z sao cho z 2 là số thuần ảo là hai đường thẳng d1 ; d2. Góc α giữa 2 đường thẳng d1 ; d2 là bao nhiêu?
Xem lời giải »
Câu 6:
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z + 2| + |z – 2| = 5 trên mặt phẳng tọa độ là một
Xem lời giải »