Cho tam giác ABC cân tại A. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Điểm I đối xứng với F qua E. Chứng minh tứ giác BDEC là hình thang cân.
Câu hỏi:
Cho tam giác ABC cân tại A. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Điểm I đối xứng với F qua E. Chứng minh tứ giác BDEC là hình thang cân.
Trả lời:
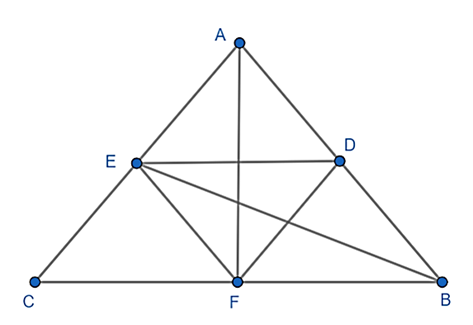
Xét ΔABC, ta có:
AD = DB (gỉa thiết)
AE = EC (gỉa thiết)
⇒ DE là đường trung bình của ΔABC
⇒ DE // BC
⇒ Tứ giác DECB là hình thang
mà (vì ΔABC cân tại A)
⇒ Tứ giác DECB là hình thang cân.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Chứng minh rằng A = 1.5 + 2.6 + 3.7 + … + 2023.2027 chia hết cho 11, 23 và 2023.
Xem lời giải »
Câu 4:
Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD
a) Chứng minh rằng AF // CE.
b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.
Xem lời giải »
Câu 6:
Cho tam giác ABC có trung tuyến AM , Gọi I là trung điểm AM , D là giao điểm BI và AC. Chứng minh AD = .
Xem lời giải »
Câu 7:
Tìm điều kiện của tham số m dể phương trình cos2x − 4cosx + m = 0 có nghiệm.
Xem lời giải »


