Cho tam giác ABC vuông tại A, đường cao AH biết BH = 3.6 cm; CH = 6.4 cm a) Tính AH, AB và số đo góc hca

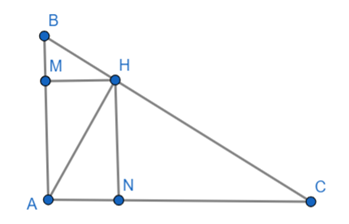
a) Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH² = BH.CH = 3,6 . 6,4 = 23,04

Suy ra: AH = 4,8 cm

AB² = AH² + HB² = 4,8² + 3,6²

⇒ AB = 6 cm

AC = $\sqrt{A{H}^2+H{C}^2}=8\left(cm\right)$

$\tan \widehat{HCA}=\tan \widehat{ACB}=\frac{AB}{AC}=\frac{6}{8}$

⇒ $\widehat{HCA}\approx 36,9°$

b) Xét tam giác AMH và tam giác AHB có:

Chung $\widehat{A}$

$\widehat{AMH}=\widehat{AHB}=90°$

⇒ ∆AMH ~ ∆AHB (g.g)

⇒ $\frac{AM}{AH}=\frac{AH}{AB}$

⇒ AM.AB = AH² (1)

Chứng minh tương tự: ∆ANH ~ ∆AHC (g.g)

⇒ $\frac{AN}{AH}=\frac{AH}{AC}$

⇒ AN.AC = AH² (2)

Từ (1) và (2): AM.AB = AN.AC.