Cho tam giác ABC, gọi BM và CN lần lượt là các đường trung tuyến sao cho BM vuông góc với CN. Chứng minh cotA = 2 (cotB + cotC).

Câu hỏi:

Trả lời:

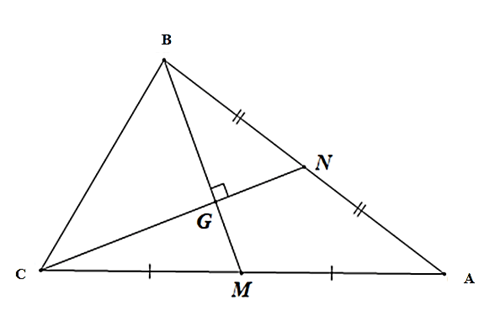
Theo định lý cosin: cosA = $\frac{b^{2} + c^{2} - a^{2}}{2 b c}$

Và sinA = $\frac{a}{2 R}$

cotA = $\frac{\cos A}{\sin A} = \frac{b^{2} + c^{2} - a^{2}}{2 b c} : \frac{a}{2 R} = \frac{b^{2} + c^{2} - a^{2}}{a b c} . R = \frac{b^{2} + c^{2} - a^{2}}{4 S}$ (*)

Lại có theo công thức tính độ dài đường trung tuyến của tam giác ta có:

BM² = $\frac{a^{2} + c^{2}}{2} - \frac{b^{2}}{4}$

CN² = $\frac{c^{2} + b^{2}}{2} - \frac{a^{2}}{4}$

Suy ra: a² = BC² = BG² + GC² = $\frac{4}{9} B M^{2} + \frac{4}{9} C N^{2}$ = $\frac{4}{9} (\frac{a^{2} + c^{2}}{2} - \frac{b^{2}}{4}) + \frac{4}{9} (\frac{c^{2} + b^{2}}{2} - \frac{a^{2}}{4})$

⇔ a² = $\frac{4}{9} (\frac{b^{2} + c^{2}}{4} + a^{2})$

⇔ 9a² = b² + c² + 4a²

⇔ 5a² = b² + c² (**)

Thay (**) vào (*): cotA = $\frac{5 a^{2} - a^{2}}{4 S} = \frac{4 a^{2}}{4 S} = \frac{a^{2}}{S} (1)$

Mặt khác cotB + cotC = $\frac{a^{2} + c^{2} - b^{2}}{4 S} + \frac{a^{2} + b^{2} - c^{2}}{4 S}$

⇒ cotB + cotC = $\frac{2 a^{2}}{4 S} = \frac{a^{2}}{2 S}$ (2)

Từ (1) và (2) suy ra: cotA = 2 (cotB+cotC) = $\frac{a^{2}}{S}$

Vậy cotA = 2 (cotB + cotC).

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Chứng minh rằng A = 1.5 + 2.6 + 3.7 + … + 2023.2027 chia hết cho 11, 23 và 2023.

Xem lời giải »

Câu 2:

Chứng minh rằng $\frac{2}{\sin 4 x} - \tan 2 x = \cot 2 x$ .

Xem lời giải »

Câu 3:

Tìm x biết:

x - \sqrt{x - 1} = 3

Xem lời giải »

Câu 4:

Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD

a) Chứng minh rằng AF // CE.

b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.

Xem lời giải »

Câu 5:

Chứng tỏ rằng các số có dạng $\bar{a a}$ chia hết cho 11.

Xem lời giải »

Câu 6:

Tìm 2 số tự nhiên nhỏ nhất a và b thỏa mãn ƯCLN(a, b) = 12 và a – b = 84.

Xem lời giải »

Câu 7:

Cho ba số x, y, z thỏa mãn x² + y² + z² = xy + yz + zx và x + y + z = -3. Tính giá trị biểu thức B = x²⁰²² + y²⁰²³ + z²⁰²⁴.

Xem lời giải »

Câu 8:

Viết $\frac{3}{2}$ thành 3 phân số thập phân rồi chuyển 3 phân số đó thành số thập phân.

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho tam giác ABC, gọi BM và CN lần lượt là các đường trung tuyến sao cho BM vuông góc với CN. Chứng minh cotA = 2 (cotB + cotC).

Xem thêm bài tập Toán có lời giải hay khác: