Cho tam giác ABC. Vẽ các tam giác đều ABM, ACN phía ngoài
Câu hỏi:
Cho tam giác ABC. Vẽ các tam giác đều ABM, ACN phía ngoài tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, AM, AN. Chứng minh tam giác DEF đều.
Trả lời:
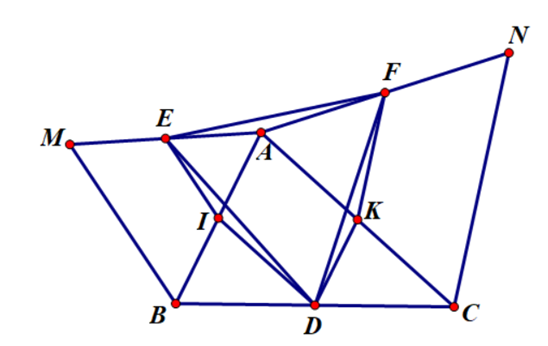
Gọi I là trung điểm AB
Ta có: EI là đường trung bình của tam giác AMB
⇒ EI // MB
⇒ \(\widehat {AEI} = \widehat {AMB} = 60^\circ \)
Lại có: EI = \(\frac{1}{2}MB = AE;ID = \frac{1}{2}AC = AF\)
\(\widehat {EAF} = 360^\circ - 2.60^\circ - \widehat {BAC} = 240^\circ - \widehat {BAC}\)
\(\widehat {EID} = 360^\circ - 120^\circ - \widehat {BID} = 240^\circ - \widehat {BAC}\)(\(\widehat {BID} = \widehat {BAC}\) vì ID // AC)
Xét ∆EID và ∆AEF có:
EI = AE
\[\widehat {EID} = \widehat {EAF}\]
ID = AF
Suy ra: △EID = △ EAF (c.g.c)
⇒ DE = EF (*) và \(\widehat {IED} = \widehat {AEF}\)
Mà \(\widehat {AEI} = \widehat {IED} + \widehat {DAE} = 60^\circ \)
⇒ \(\widehat {AEF} + \widehat {DAE} = 60^\circ \) hay \(\widehat {DEF} = 60^\circ \)(**)
Từ (*) và (**) suy ra: DEF là tam giác đều.