Cho tam giác đều ABC. Gọi M là điểm thuộc cạnh BC. Gọi E, F lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC.
Câu hỏi:
Cho tam giác đều ABC. Gọi M là điểm thuộc cạnh BC. Gọi E, F lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC. Gọi I là trung điểm của AM, D là trung điểm của BC.
a, Tính góc DIE và góc DIF.
b, Chứng minh rằng: tứ giác DEIF là hình thoi.
Trả lời:
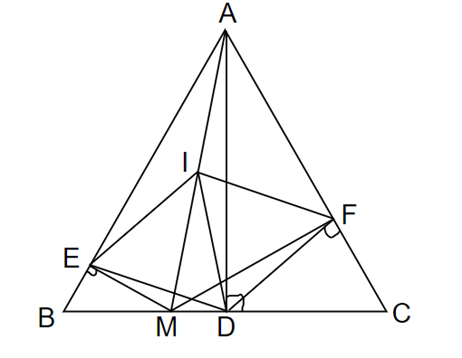
a) ΔAME vuông tại E có đường trung tuyến EI
⇒ EI = 12AM ⇒ EI = MI = AI
+ Tương tự ta có: DI = FI = AI = MI
Tam giác AEI cân tại I nên ^IAE=^IEA
⇒ ^EIM=2^IAE
Tương tự: ^MID=2^IAD
⇒ ^EIM+^MID=2^IAE+2^IAD
^DIE=2.30° (do góc )
(do )
Suy ra:
b) Tam giác DIE có: DI = EI mà nên tam giác DIE đều
Suy ra: DI = EI = DE (1)
Tương tự: tam giác DIF đều vì DI = FI mà
Suy ra: DI = FI = DF (2)
Từ (1) và (2) ⇒ DE = EI = IF = DF
⇒ tứ giác DEIF là hình thoi.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính
Xem lời giải »
Câu 2:
Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, . Bán kính đường tròn nội tiếp tam giác ABC là cm. Tính đường cao AH của tam giác ABC.
Xem lời giải »
Câu 3:
Cho C = 5 + 52 + … + 520. Chứng minh rằng C chia hết cho 5, 6, 13.
Xem lời giải »
Câu 5:
Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.
Xem lời giải »
Câu 6:
Tìm x sao cho: (x + 5)(4 − 3x) − (3x + 2)2 + (2x + 1)3 = (2x − 1)(4x2 + 2x + 1).
Xem lời giải »
Câu 8:
Tìm các số tự nhiên n sao cho 6n + 16 chia hết cho n + 2.
Xem lời giải »
