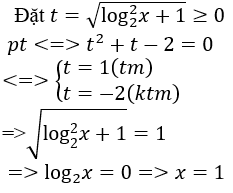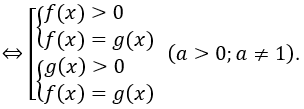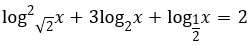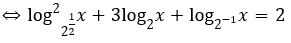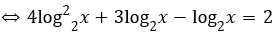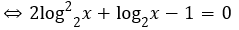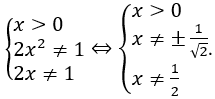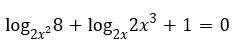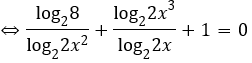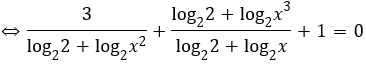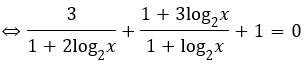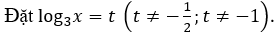Giải phương trình logarit bằng cách đặt ẩn phụ cực hay - Toán lớp 12

---

Giải phương trình logarit bằng cách đặt ẩn phụ cực hay

Với Giải phương trình logarit bằng cách đặt ẩn phụ cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giải phương trình logarit bằng cách đặt ẩn phụ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

1. Phương trình lôgarit cơ bản

    • log_ax = b ⇔ x = a^b (0 < a ≠ 1).

    • log_af(x)=log_ag(x)

2. Các bước giải phương trình bằng phương pháp đặt ẩn phụ

Giải phương trình: f[log_ag(x)] = 0 (0 < a ≠ 1).

    • Bước 1: Đặt t = log_ag(x) (*).

    • Bước 2: Tìm điều kiện củat (nếu có).

    • Bước 3: Đưa về giải phương trình f(t) = 0 đã biết cách giải.

    •Bước 4: Thay vào (*) để tìm x.

3. Một số lưu ý quan trọng khi biến đổi

    1) log_af²(x) = 2log_a|f(x)|

    2) log_af^2k(x) = 2klog_a|f(x)|

    3) log_af^2k+1(x) = (2k+1)log_af(x)

    4) log_a(f(x)g(x)) = log_a|f(x)| + log_a|g(x)|

Ví dụ minh họa

Bài 1: Giải phương trình log²₃ x - 4log₃x + 3 = 0.

Hướng dẫn:

Điều kiện của phương trình là x > 0.

Đặt log₃x = t. Khi đó phương trình đã cho trở thành

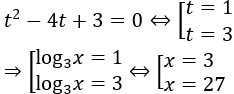
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {3;27}.

Bài 2: Giải phương trình

Hướng dẫn:

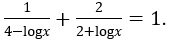
Khi đó phương trình đã cho trở thành

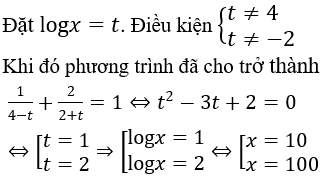
Tập nghiệm của phương trình đã cho là {10; 100}.

Bài 3: Giải phương trình

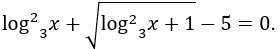
Hướng dẫn:

Điều kiện của phương trình là x > 0.

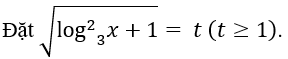
Khi đó phương trình đã cho trở thành

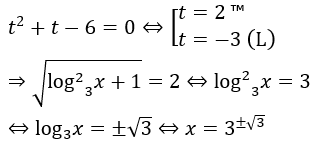
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {3^√3; 3^-√3 }.

B. Bài tập vận dụng

Bài 1: Giải phương trình

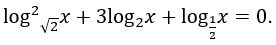
Lời giải:

Điều kiện của phương trình là x > 0.

Đặt log₂ x = t . Khi đó phương trình đã cho trở thành

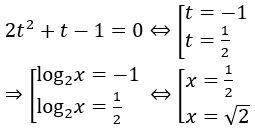
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {1/2; √2}.

Bài 2: Giải phương trình

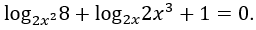
Lời giải:

Điều kiện của phương trình là

Khi đó phương trình đã cho trở thành

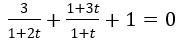
⇔ 3(t+1) + (1+3t)(1+2t) + (1+2t)(1+t) = 0

⇔ 8t² + 11t + 5 = 0 ⇒ VN

Vậy phương trình đã cho vô nghiệm.

Bài 3: Giải phương trình

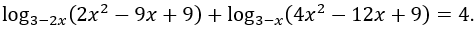
Lời giải:

Điều kiện của phương trình là

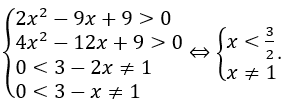
Khi đó phương trình:

log_3-2x(2x²-9x+9)+log_3-x (4x²-12x+9)=4

⇔ log_3-2x(x-3)(2x-3)+log_3-x (2x-3)²=4

⇔ log_3-2x|x-3|+log_3-2x|2x-3|+2log_3-x |2x-3|=4

⇔ log_3-2x(3-x)+log_3-2x(3-2x)+2log_3-x (3-2x)=4

⇔ log_3-2x(3-x)+1+2log_3-x (3-2x)=4

⇔ log_3-2x(3-x)+2log_3-x (3-2x)-3=0

Đặt log_3-2x(3-x) = t. Khi đó phương trình đã cho trở thành:

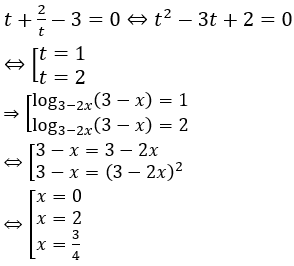
Kết hợp điều kiện ta được nghiệm phương trình là

Bài 4: Giải phương trình

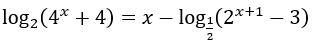
Lời giải:

Điều kiện: 2^x+1 - 3 > 0 ⇔ x > log₂ 3 - 1.

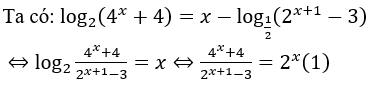
Đặt t=2^x, t > 0. Ta có (1) ⇒ t²+4 = 2t²-3t ⇔ t²-3t-4 = 0 ⇒ t = 4.

⇔ 2^x = 2² ⇔ x = 2 (thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là x=2.

Bài 5: Giải phương trình

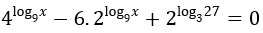
Lời giải:

Điều kiện: x > 0.

Ta có phương trình tương đương 2^2log₉x - 6.2^log₉x + 2³ = 0. (1)

Đặt t = 2^log₉x,t > 0. (1) ⇒ t²-6t+8=0

Với t = 2 ⇔ 2^{log₉ x} = 2 ⇔ log₉ x = 1 ⇔ x = 9.

Với t = 4 ⇔ 2^{log₉ x} = 2² ⇔ log₉ x = 2 ⇔ x = 81.

Vậy tập nghiệm của phương trình đã cho là S={9;81}.

Bài 6: Giải phương trình

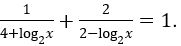
Lời giải:

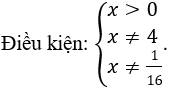
Đặt t=log₂ x, điều kiện

Khi đó phương trình trở thành:

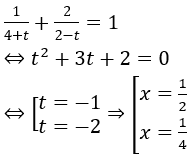
Bài 7: Giải phương trình

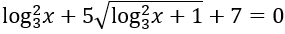
Lời giải:

Đk: x > 0

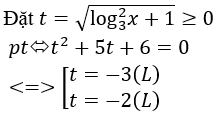
Vậy phương trình vô nghiệm.

Bài 8: Giải phương trình

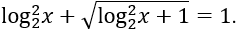
Lời giải:

Đk: x > 0