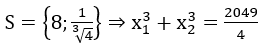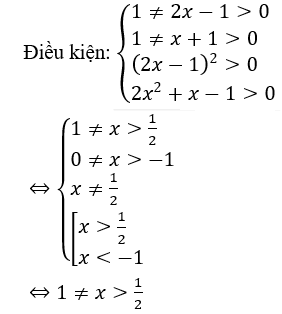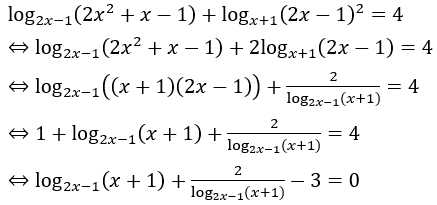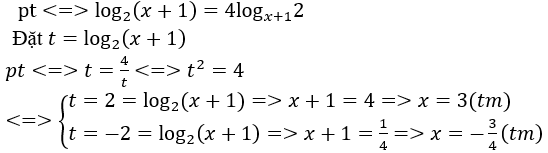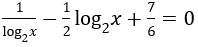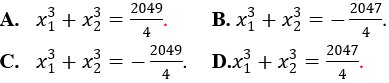Trắc nghiệm giải phương trình logarit bằng cách đặt ẩn phụ - Toán lớp 12

---

Trắc nghiệm giải phương trình logarit bằng cách đặt ẩn phụ

Với Trắc nghiệm giải phương trình logarit bằng cách đặt ẩn phụ Toán lớp 12 tổng hợp 14 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình logarit bằng cách đặt ẩn phụ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Phương trình log₃(3^x-1).log₃(3^x+1-3) = 6 có:

A. Hai nghiệm dương.        B. Một nghiệm dương.

C. Phương trình vô nghiệm        D. Một nghiệm kép

.

Lời giải:

Đáp án : A

Giải thích :

Tập xác định 3^x-1 > 0 ⇔ x > 0.

log₃(3^x-1).log₃(3^x+1-3) = 6 ⇔ log₃(3^x-1).log₃(3(3^x-1))=6 ⇔ log₃(3^x-1).(1+log₃(3^x-1))-6=0.

Đặt log₃(3^x-1) = t

Khi đó phương trình trở thành

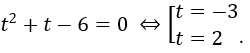
Suy ra phương trình đã cho có hai nghiệm dương.

Bài 2: Phương trình log₃(√x+2) = log₇ x có nghiệm là:

A.x=4        B.x=49        C.x=25        D. Đáp án khác.

Lời giải:

Đáp án : B

Giải thích :

Tập xác định x > 0.

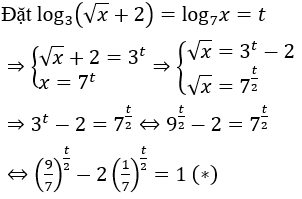
Phương trình (*) có một nghiệm t=2 .

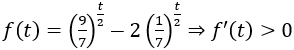
Suy ra vế trái của (*) là hàm đồng biến mà vế phải là hàm hằng nên(*) có nghiệm duy nhất t=1⇒x=49.

Bài 3: Tìm nghiệm của phương trình sau: log_2x-1 (2x²+x-1)+log_x+1 (2x-1)² = 4

A. x=2        B.x=5/2

C. x=5/4        D. Cả A và C đều đúng.

Lời giải:

Đáp án : D

Giải thích :

Đặt log_2x-1(x+1)=t (t ≠ 0).

Khi đó phương trình đã cho trở thành:

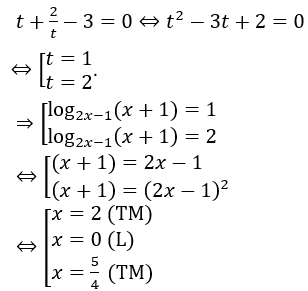
Bài 4: Tìm số nghiệm của phương trình log₂²x+3log₂x+2 = 0.

A. 2 nghiệm.        B. 1 nghiệm.        C. Vô nghiệm.        D. 3 nghiệm.

Lời giải:

Đáp án : A

Giải thích :

• Tự luận: Đk: x > 0

Đặt t=log₂x

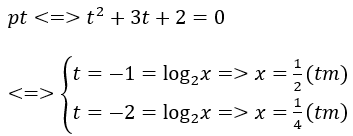
Bài 5: Tìm số nghiệm của phương trình log₂²(x²-1)+log₂(x-1)+log₂(x+1)-2=0.

A. 4 nghiệm.        B. 1 nghiệm.        C. 2 nghiệm.        D. 3 nghiệm.

Lời giải:

Đáp án : C

Giải thích :

• Tự luận:

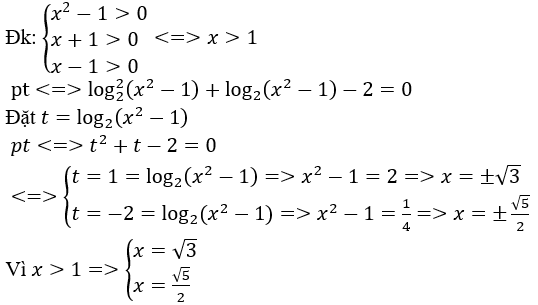
Bài 6: Tìm số nghiệm của phương trình log₂(x+1)=log_x+1 16.

A. Vô nghiệm.        B. 3 nghiệm.        C. 1 nghiệm.        D. 2 nghiệm.

Lời giải:

Đáp án : D

Giải thích :

• Tự luận:

Bài 7: Tìm số nghiệm của phương trình log_x 2 - log₄ x + 7/6 = 0.

A. 2 nghiệm.        B. 1 nghiệm.        C. 4 nghiệm.        D. 3 nghiệm.

Lời giải:

Đáp án : A

Giải thích :

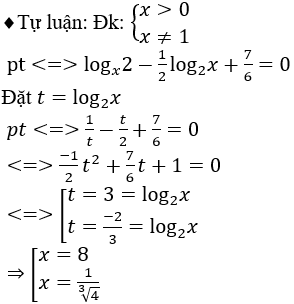
Bài 8: Tìm số nghiệm của phương trình log₂²x+(x-12)log₂x+11-x=0.

A. Vô nghiệm.        B. 3 nghiệm.        C.1 nghiệm.        D. 2 nghiệm.

Lời giải:

Đáp án : D

Giải thích :

• Tự luận: Đk: x > 0

Đặt t=log₂x

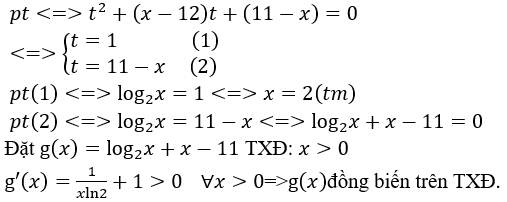
Mà g(3)=0 ⇒ x=3 là nghiệm duy nhất của pt (2).

Vậy phương trình có hai nghiệm.

Bài 9: Nếu đặt t=log₂x thì phương trình sau trở thành phương trình nào?

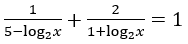
A. t²-5t+6=0.        B. t²+5t+6=0.        C. t²-6t+5=0.        D. t²+6t+5=0.

Lời giải:

Đáp án : A

Giải thích :

Đặt t=log₂x

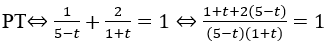
⇔ 1+t+2(5-t) = (5-t)(1+t)

⇔ 11-t = 5+4t-t²⇔ t²-5t+6=0.

Bài 10: Nếu đặt t=lgx thì phương trình sau trở thành phương trình nào?

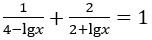
A. t²+2t+3=0.        B. t²-3t+2=0.        C. t²-2t+3=0.        D. t²+3t+2=0.

Lời giải:

Đáp án : B

Giải thích :

Đặt t=lgx

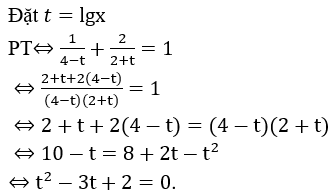
Bài 11: Nếu đặt t=log₂xthì phương trình log₂(4x)-log_x 2=3 trở thành phương trình nào?

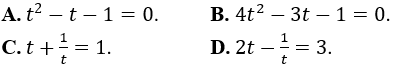
Lời giải:

Đáp án : A

Giải thích :

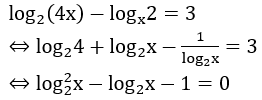
Bài 12: Nếu đặt t=logxthì phương trình log²x³-20log√x+1=0trở thành phương trình nào?

A. 9t²-20√t+1=0.        B. 3t²-20t+1=0.

C. 9t²-10t+1=0.        D. 3t²-10t+1=0.

Lời giải:

Đáp án : C

Giải thích :

log²x³ - 20log√x+1 = 0 ⇔ 9log²x - 10logx+1 = 0

Bài 13: Phương trình x^ln7 + 7^lnx = 98 có nghiệm là:

A. x=e.        B. x=2.        C. x=e².        D. x=√e.

Lời giải:

Đáp án : C

Giải thích :

[Phương pháp tự luận]

Điều kiện : x > 0; x ≠ 1

Đặt x = e^t

x^ln7 + 7^lnx = 98 ⇔ e^t.ln7 + 7^lnet = 98 ⇔ 2.7^t = 98 ⇔ t = 2

[Phương pháp trắc nghiệm]

Lần lượt thay x=2; x=e; x=√e vào phương trình ta được đẳng thức sai, vậy loại A, B, D, vậy chọn đáp án C.

Bài 14: Biết phương trình sau có hai nghiệm x₁,x₂. Khẳng định nào sau đây là đúng?

Lời giải:

Đáp án : A

Giải thích :

Đặt t=log₂x. Phương trình đã cho trở thành 3t²-7t-6 = 0.

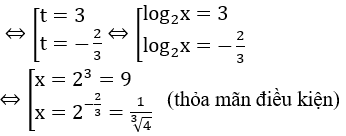
Vậy tập nghiệm của phương trình đã cho là