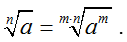Lý thuyết Lũy thừa - Toán lớp 12

Lý thuyết Lũy thừa

Tài liệu Lý thuyết Lũy thừa Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Lũy thừa từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

1. Định nghĩa lũy thừa và căn

    • Cho số thực b và số nguyên dương n (n ≥ 2) . Số a được gọi là căn bậc n của số b nếu aⁿ = b .

    • Chú ý: - Với n lẻ và b ∈ R : Có duy nhất một căn bậc n của b, kí hiệu là ⁿ√b .

    - Với n chắn:

        +) b < 0: Không tồn tại căn bậc n của b.

        +) b = 0: Có một căn bậc n của b là số 0.

        +) b > 0: Có hai căn bậc n của a là hai số đối nhau, căn có giá trị dương ký hiệu là ⁿ√b, căn có giá trị âm kí hiệu là -ⁿ√b.

Số mũ α	Cơ số a	Lũy thừa aα
α = n ∈ N*	a ∈ R	aα = an = a.a. ... .a (n thừa số a)
α = 0	a ≠ 0	aα = a0 = 1
α = -n (n ∈ N*)	a ≠ 0	aα = a0 = 1/an
α = m/n	a > 0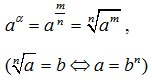
α = lim rn (rn ∈ Q, n ∈ N*)	a > 0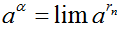

2. Một số tính chất của lũy thừa

    • Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:

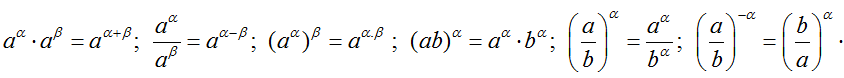
    • Nếu a > 1 thì a^α > a^β ⇔ α > β ; Nếu ) < a < 1 thì a^α > a^β ⇔ α < β .

    • Với mọi 0 < a < b, ta có: a^m < b^m ⇔ m > 0; a^m > b^m ⇔ m < 0 ;

    • Chú ý: - Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.

    - Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

    - Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.

3. Một số tính chất của căn bậc n

    • Với a, b ∈ R; n ∈ N*, ta có:

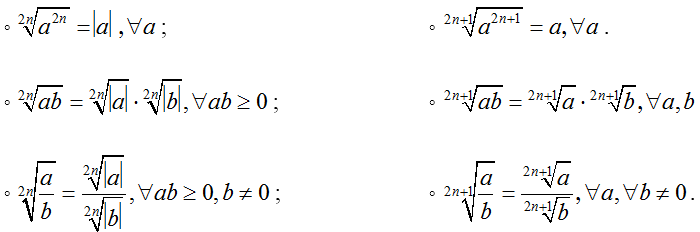
    • Với a, b ∈ R ta có:

    , ∀ a > 0, n nguyên dương, m nguyên

    , ∀ a ≥ 0, n, m nguyên dương

    , ∀ a > 0, m,n nguyên dương, p, q nguyên. Đặc biệt

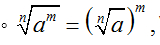
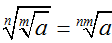
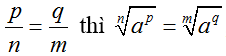
B. Kĩ năng giải bài tập

1. Vận dụng thành thạo định nghĩa, tính chất của lũy thừa với số mũ hữu tỉ.

2. Công thức lãi kép.

    a) Định nghĩa: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước cộng với phần lãi của kì trước.

    b) Công thức: Giả sử số tiền gốc là A; lãi suất r%/kì hạn gửi (có thể là tháng, quý hay năm).

    ● Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A(1 + r)ⁿ

    ● Số tiền lãi nhận được sau n kì hạn gửi là A(1 + r)ⁿ - A = A[(1 + r)ⁿ - 1]

    c) Ví dụ: Bà Hoa gửi 100 triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8%/năm. Tính số tiền lãi thu được sau 10 năm.

    Lời giải

    Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hoa thu về là:

    A(1 + r)ⁿ = 100tr.(1 + 0,08)¹⁰ ≈ 215,892tr.

    Suy ra số tiền lãi bà Hoa thu về sau 10 năm là:

    A(1 + r)ⁿ - A = 100tr(1 + 0,08)¹⁰ - 100tr = 115,892tr.