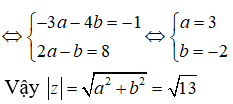Môđun của số phức z thỏa mãn điều kiện (3z - z−)(1 + i) - 5z = 8i - 1 là 1

Câu hỏi:

Môđun của số phức z thỏa mãn điều kiện $(3 z - z) (1 + i) - 5 z = 8 i - 1$ là

A. 1

B. 5

C. $\sqrt{13}$

D. 13

Trả lời:

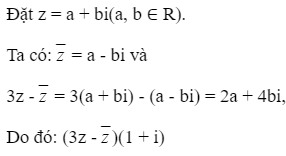
= 2a - 4b + (2a + 4b)i

Theo giả thiết: (2a - 4b) + (2a + 4b)i - 5(a + bi) = 8i - 1

⇔ -3a - 4b + (2a - b)i = -1 + 8i

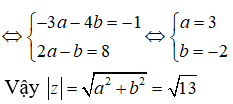
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Chọn C

Câu 1:

Cho hai số phức $z_{1} = 1 + 2 i, z_{2} = 2 - 3 i .$ Phần thực và phần ảo của số phức $w = 3 z_{1} - 2 z_{2}$ là

Câu 2:

Phần thực và phần ảo của số phức $z = {(1 + \sqrt{3} i)}^{2}$ là

Câu 3:

Phần ảo của số phức $z = i (1 + \sqrt{3} i)^{3}$ là

Câu 4:

Thực hiện phép tính: $T = \frac{2 + 3 i}{1 + i} + \frac{3 - 4 i}{1 - i} + i (4 + 9 i)$ ta có

Câu 5:

Cho số phức z thỏa mãn: $i . z + z = 2 + 2 i$ và $z . z = 2 .$ Khi đó $z^{2}$ bằng:

Câu 6:

Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: $w = \frac{z - 2 z + 1}{z^{2}}$ là

Câu 7:

Cho số phức z thỏa mãn $5 \frac{(z + i)}{z + 1} = 2 - i .$ Khi đó môđun của số phức $w = 1 + z + z^{2}$ là

Câu 8:

Phương trình $z^{2} - 2 z + 3 = 0$ có các nghiệm là

Các dạng bài tập Toán lớp 12