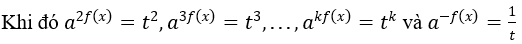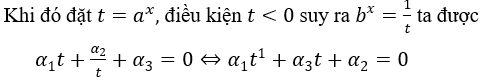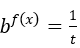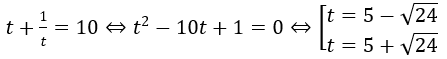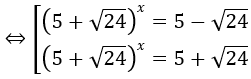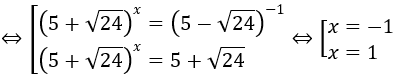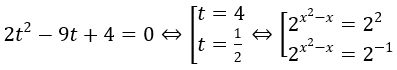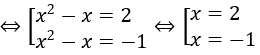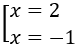Phương pháp đặt ẩn phụ trong phương trình mũ cực hay - Toán lớp 12

---

Phương pháp đặt ẩn phụ trong phương trình mũ cực hay

Với Phương pháp đặt ẩn phụ trong phương trình mũ cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương pháp đặt ẩn phụ trong phương trình mũ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

    Ta thường sử dụng 1 ẩn phụ để chuyển phương trình ban đầu thành 1 phương trình với 1 ẩn phụ.

Các phép đặt ẩn phụ thường gặp sau:

Dạng 1: Phương trình α_k + α_k-1 a^(k-1)x + ... + α₁ a^x + α⁰ = 0

        Khi đó ta đặt t = a^x điều kiện t > 0, ta được α_k t^k + α_k-1 t^k-1 + ... + α₁ t + α₀ = 0

        Mở rộng: Nếu đặt t = a^f(x) , điều kiện hẹp t > 0.

       

Dạng 2: Phương trình α₁ a^x + α₂ a^x + α₃ = 0 với a.b = 1

       

        Mở rộng: Với a.b = 1 thì khi đặt t = a^f(x), điều kiện hẹp t > 0, suy ra

Dạng 3: Phương trình α₁ a^2x + α₂ (a.b)^x + α₃ b^2x = 0 khi đó chia hai vế của phương trình cho b^2x > 0 (hoặc a^2x, (a.b)^x), điều kiện t < 0, ta được

        , điều kiện t < 0 , ta được α₁ t² + α₂ t+α₃ = 0

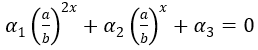
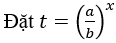
        Mở rộng: Với phương trình mũ có chứa các nhân tử: a^2f, b^2f, (a.b)^2f, ta thực hiện theo các bước sau:

            + Chia 2 vế của phương trình cho b^2f > 0 (hoặc a^2f,(a.b)^f)

            + Đặt 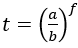điều kiện hẹp t > 0

Ví dụ minh họa

Bài 1: Giải phương trình 9^x-5.3^x+6=0

Hướng dẫn:

Đặt t=3^x (t > 0), khi đó phương trình đã cho tương đương với

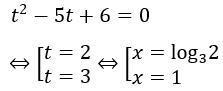
Bài 2: Giải phương trình sau: (7+4√3)^x-3(2-√3)^x+2=0

Hướng dẫn:

Nhận xét rằng 7+4√3=(2+√3)²; (2+√3)(2-√3)=1

Do đó nếu đặt t=(2+√3)^x điều kiện t > 0 thì (2-√3)^x=1/t và (7+4√3)^x = t²

Khi đó phương trình đã cho tương đương với

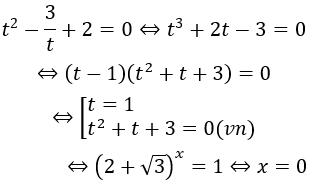
Vậy phương trình có nghiệm x=0

Bài 3: Giải phương trình sau: (√2-1)^x+(√2+1)^x-2√2=0

Hướng dẫn:

Đặt t=(√2+1)^x ta có phương trình đã cho tương đương:

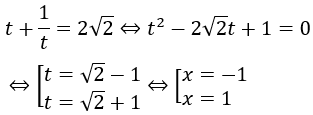
Bài 4: Giải phương trình sau: (3+√5)^x+16(3-√5)^x = 2^x+3

Hướng dẫn:

Chia cả hai vế của phương trình cho 2^x > 0, ta được

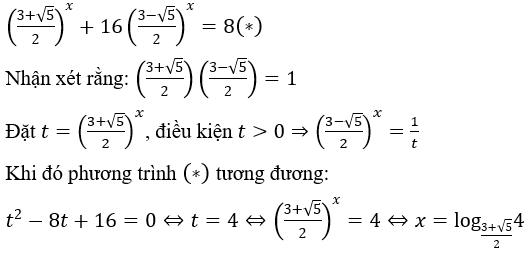
B. Bài tập vận dụng

Bài 1: Giải phương trình sau:

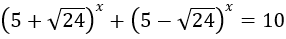
Lời giải:

Nhận xét rằng (5+√24)(5-√24) = 1

Đặt t = (5+√24)^x, điều kiện t > 0 ⇒ (5-√24)^x = 1/t

Khi đó phương trình đã cho tương đương:

Bài 2: Giải phương trình sau:

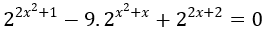
Lời giải:

Chia cả hai vế của phương trình cho 2^2x+2 ≠ 0 ta được:

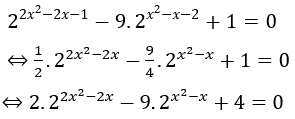
Đặt t = 2^x2-x điều kiện t > 0. Khi đó phương trình đã cho tương đương với

Vậy phương trình có hai nghiệm

Bài 3: Giải phương trình sau:

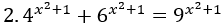
Lời giải:

Biến đổi phương trình về dạng:

2.2^2(x2+1) +(2.3)^(x2+1)=3^2(x2+1)

Chia cả hai vế của phương trình cho 2^2(x2+1) ≠ 0, ta được:

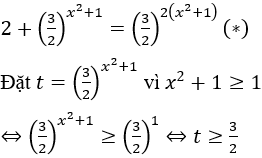
Khi đó phương trình có dạng:

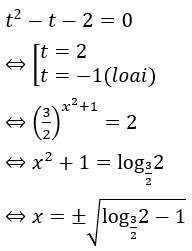
Bài 4: Giải phương trình sau:

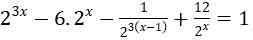
Lời giải:

Viết lại phương trình có dạng:

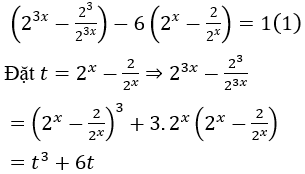
Khi đó phương trình (1) có dạng:

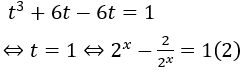
Đặt u = 2^x, u > 0. Khi đó phương trình (2) có dạng:

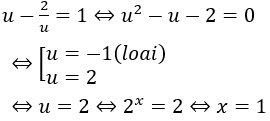
Vậy phương trình có nghiệm x=1

Bài 5: Giải phương trình sau:

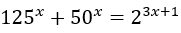
Lời giải:

Biến đổi phương trình về dạng:

125^x+50^x = 2.8^x

Chia cả 2 về của phương trình trên cho 8^x ≠ 0, ta được:

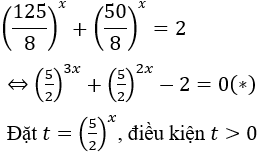
Khi đó phương trình (*) tương đương:

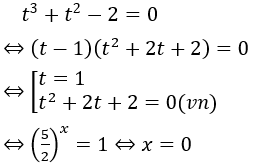
Bài 6: Giải phương trình sau:

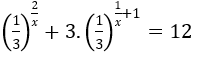
Lời giải:

Biến đổi phương trình về dạng:

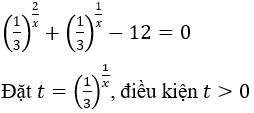
Khi đó phương trình đã cho có dạng:

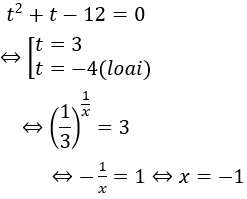
Bài 7: Giải phương trình sau:

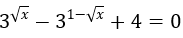
Lời giải:

Điều kiện x ≥ 0. Biến đổi phương trình về dạng:

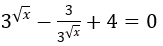
Đặt t=3^√x, điều kiện t ≥ 1

Khi đó phương trình đã cho tương đương:

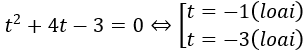
Vậy phương trình đã cho vô nghiệm.

Bài 8: Giải phương trình sau:

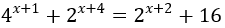
Lời giải:

Đưa phương trình về dạng: 2^2(x+1) + 2^x+4 = 2^x+2 + 16 ⇔ 2.2^2x - 6.2^x - 8 = 0

Đặt t = 2^x, điều kiện t > 0

Khi đó phương trình đã cho tương đương:

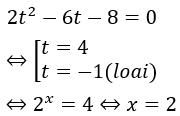
Bài 9: Giải phương trình sau:

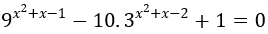
Lời giải:

Đưa phương trình đã cho về dạng:

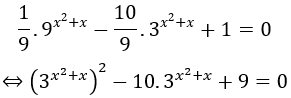
Đặt t = 3^x2+x, t > 0

Phương trình đã cho tương đương:

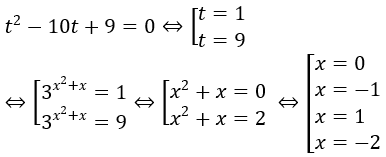
Bài 10: Giải phương trình sau:

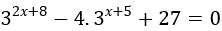
Lời giải:

Biến đổi phương trình đã cho về dạng:

3⁸.3^2x-4.3⁵.3^x+27=0 ⇔ 6561.(3^x )²-972.3^x+27 = 0

Đặt t = 3^x, t > 0

Phương trình đã cho tương đương:

Bài 11: Giải phương trình sau:

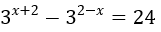
Lời giải:

Biến đổi phương trình đã cho về dạng:

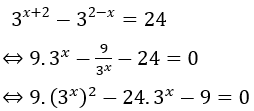
Đặt t = 3^x, t > 0

Phương trình đã cho tương đương:

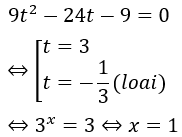
Vậy phương trình có nghiệm x=1