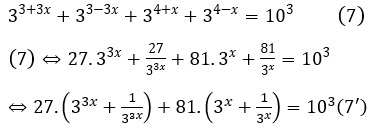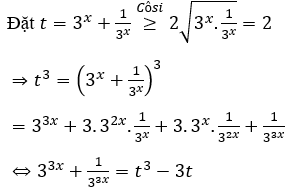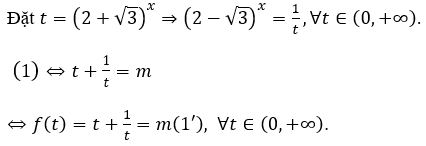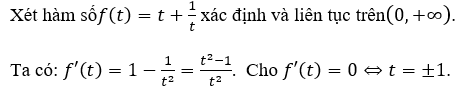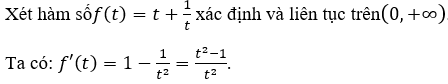Trắc nghiệm Sử dụng tính đơn điệu để giải phương trình mũ - Toán lớp 12

---

Trắc nghiệm Sử dụng tính đơn điệu để giải phương trình mũ

Với Trắc nghiệm Sử dụng tính đơn điệu để giải phương trình mũ Toán lớp 12 tổng hợp 16 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Sử dụng tính đơn điệu để giải phương trình mũ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Phương trình (√3-√2)^x+(√3+√2)^x=(√10)^x có tất cả bao nhiêu nghiệm thực ?

A. 1.        B. 2.        C. 3.        D. 4.

Lời giải:

Đáp án : B

Giải thích :

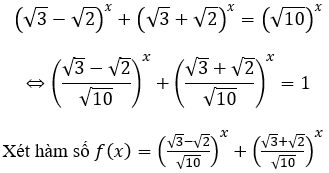
Ta có: f(2)=1

Hàm số f(x) nghịch biến trên R

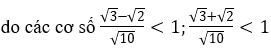
Vậy phương trình có nghiệm duy nhất là x=2.

Bài 2: Phương trình 3^2x+2x(3^x+1)-4.3^x-5=0 có tất cả bao nhiêu nghiệm không âm ?

A. 1.        B.2.        C.0.        D. 3.

Lời giải:

Đáp án : A

Giải thích :

3^2x+2x(3^x+1)-4.3^x-5=0 ⇔ (3^2x-1)+2x(3^x+1)-(4.3^x+4)=0

⇔ (3^x-1)(3^x+1)+(2x-4)(3^x+1)=0 ⇔ (3^x+2x-5)(3^x+1)=0 ⇔ 3^x+2x-5=0

Xét hàm số f(x)=3^x+2x-5 , ta có: f(1)=0.

f'(x)=3^x ln3+2 > 0; ∀x ∈ R . Do đó hàm số f(x) đồng biến trên R.

Vậy nghiệm duy nhất của phương trình là x=1

Bài 3: Phương trình 3^2x+2x(3^x+1)-4.3^x-5=0 có tất cả bao nhiêu nghiệm không âm ?

A. 1.        B. 2.        C. 0.        D. 3.

Lời giải:

Đáp án : D

Giải thích :

3^2x+2x(3^x+1)-4.3^x-5=0 ⇔ (3^2x-1)+2x(3^x+1)-(4.3^x+4)=0

⇔ (3^x-1)(3^x+1)+(2x-4)(3^x+1)=0 ⇔ (3^x+2x-5)(3^x+1)=0 ⇔ 3^x+2x-5=0

Xét hàm số f(x)=3^x+2x-5, ta có: f(1)=0.

f'(x)=3^x ln3+2 > 0; ∀x ∈ R . Do đó hàm số f(x) đồng biến trên R.

Vậy nghiệm duy nhất của phương trình là x=1

Bài 4: Với giá trị của tham số m thì phương trình (m+1)16^x-2(2m-3) 4^x+6m+5=0 có hai nghiệm trái dấu?

A.-4 < m < -1.        B. Không tồn tại m.

C. -1 < m < 3/2.        D. -1 < m < -5/6.

Lời giải:

Đáp án : A

Giải thích :

Đặt 4^x=t > 0. Phương trình đã cho trở thành:

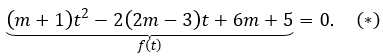
Yêu cầu bài toán ⇔ (*) có hai nghiệm t₁,t₂ thỏa mãn 0 < t₁ < 1 < t₂

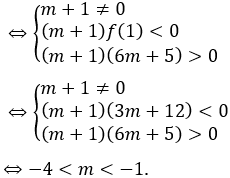
Bài 5: Tìm tất cả các nghiệm của phương trình 4^x2-3x+2 + 4^x2+6x+5 = 4^2x2+3x+7+1.

A. x ∈ {-5;-1;1;2}.        B. x ∈ {-5;-1;1;3}.

C. x ∈ {-5;-1;1;-2}.        D. x ∈ {5;-1;1;2}.

Lời giải:

Đáp án : A

Giải thích :

4^x2-3x+2+4^x2+6x+5=4^2x2+3x+7+1 ⇔ 4^x2-3x+2 + 4^x2+6x+5 = 4^x2-3x+2.4^x2+6x+5+1

⇔ 4^x2-3x+2 (1-4^x2+6x+5 )-(1-4^x2+6x+5 )=0 ⇔ (4^x2-3x+2-1)(1-4^x2+6x+5 )=0

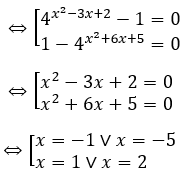
Bài 6: Phương trình 4^{sin2 x}+4^{cos2 x}=2√2 (sinx+cosx) có bao nhiêu nghiệm thuộc đoạn [0;15].

A.3.        B. 1.        C. 2.        D. 3.

Lời giải:

Đáp án : D

Giải thích :

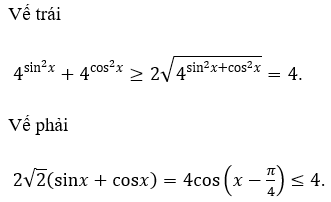
Vế trái bằng vế phải khi:

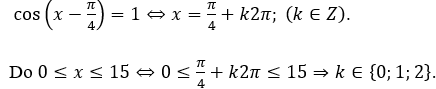
Phương trình có ba nghiệm.

Bài 7: Phương trình 3^3+3x + 3^3-3x + 3^4+x + 3^4-x = 10³ có tổng các nghiệm là ?

A. 0.        B. 2.        C. 3.        D. 4 .

Lời giải:

Đáp án : C

Giải thích :

Khi đó:

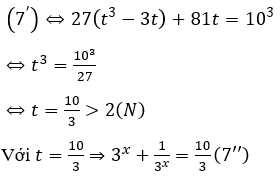
Đặt y=3^x > 0.

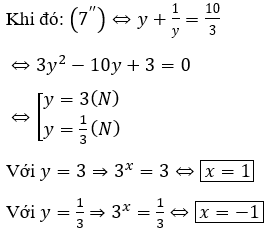
Bài 8: Tìm giá trị của tham số k để hai phương trình sau có nghiệm chung:

3^x=30-x        (1)

x-k=0        (2)

A. 2.        B. 3.        C. 4.        D. 5.

Lời giải:

Đáp án : B

Giải thích :

Phương trình(1)có nghiệm duy nhất x=3. Thay vào phương trình(2)ta được k=3.

Bài 9: Tìm tất cả các nghiệm của phương trình 4^x2-3x+2 + 4^x2+6x+5 = 4^2x2+3x+7+1.

A. x ∈ {-5;-1;1;2}.        B. x ∈ {-5;-1;1;3}.

C. x ∈ {-5;-1;1;-2}.        D. x ∈ {5;-1;1;2}.

Lời giải:

Đáp án : B

Giải thích :

4^x2-3x+2+4^x2+6x+5 = 4^2x2+3x+7+1 ⇔ 4^x2-3x+2+4^x2+6x+5=4^x2-3x+2.4^x2+6x+5+1

⇔ 4^x2-3x+2 (1-4^x2+6x+5 )-(1-4^x2+6x+5 ) = 0 ⇔ (4^x2-3x+2)-1(1-4^x2+6x+5)=0

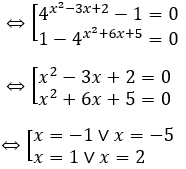
Bài 10: Phương trình 4^{sin2 x} + 4^{cos2 x} = 2√2 (sinx+cosx) có bao nhiêu nghiệm thuộc đoạn [0;15].

A.3.        B. 1.        C. 2.        D. 3.

Lời giải:

Đáp án : A

Giải thích :

Vế trái

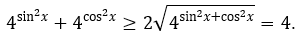
Vế phải

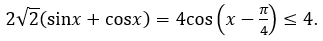
Vế trái bằng vế phải khi:

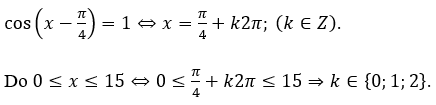
Phương trình có ba nghiệm.

Bài 11: m là tham số thay đổi sao cho phương trình 9^x - 4.3^x+1 + 27^m2-1 = 0 có hai nghiệm phân biệt. Tổng hai nghiệm đạt giá trị nhỏ nhất bằng bao nhiêu?

A. 1.        B.-3.        C. 2.        D. -4.

Lời giải:

Đáp án : B

Giải thích :

Đặt 3^x = t ta được: t²-12t+3^3(m2-1)) = 0 (1).

Do phương trình đã cho có hai nghiệm phân biệt nên (1)có hai nghiệm phân biệtt₁,t₂.

3^x₁+x₂=3^x₁.3^x₂ = t₁.t₂=3^3(m2-1) ⇒ x₁+x₂=3(m²-1) ≥ -3.

Do đó x₁+x₂ đạt giá trị nhỏ nhất bằng -3 khi m = 0.

Thay m=0 vào (1) ta được t²-12t+1/27 = 0 có hai nghiệm t₁,t₂ > 0.

Bài 12: Với giá trị nào của tham số m thì phương trình (2+√3)^x + (2-√3)^x = m có hai nghiệm phân biệt?

A. m < 2.        B. m > 2.        C.m=2.        D. m ≤ 2.

Lời giải:

Đáp án : B

Giải thích :

Nhận xét: (2+√3)(2-√3)=1 ⇔ (2+√3)^x (2-√3)^x=1.

Bảng biến thiên:

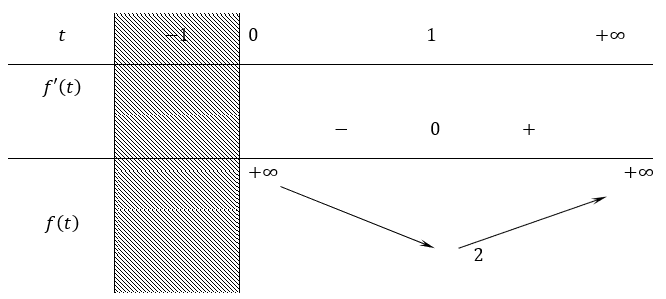
+ Nếu m > 2 thì phương trình (1') có hai nghiệm phân biệt ⇒ pt(1)có hai nghiệm phân biệt.

Bài 13: Với giá trị của tham số m thì phương trình (m+1)16^x - 2(2m-3) 4^x + 6m + 5 = 0 có hai nghiệm trái dấu?

A.-4 < m < -1.        B. Không tồn tại m.

C. -1 < m < 3/2.        D. -1 < m < -5/6.

Lời giải:

Đáp án : C

Giải thích :

Đặt 4^x=t > 0. Phương trình đã cho trở thành:

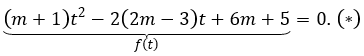
Yêu cầu bài toán ⇔ (*) có hai nghiệm t₁,t₂ thỏa mãn 0 < t₁ < 1 < t₂

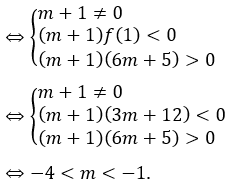
Bài 14: Với giá trị nào của tham số m thì phương trình (2+√3)^x+(2-√3)^x=m vô nghiệm?

A. m < 2.        B. m > 2.        C.m=2.        D. m ≤ 2.

Lời giải:

Đáp án : A

Giải thích :

Nhận xét: (2+√3)(2-√3)=1 ⇔ (2+√3)^x (2-√3)^x=1.

Bảng biến thiên:

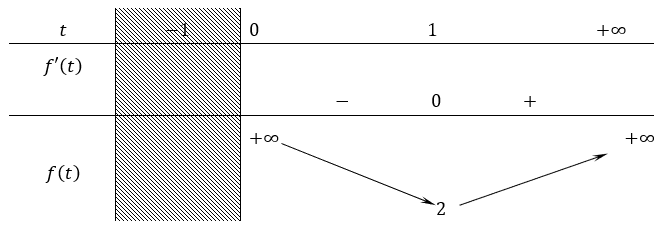
Dựa vào bảng biến thiên:

Nếu m < 2 thì phương trình (1')vô nghiệm ⇒ pt(1)vô nghiệm.

Bài 15: Với giá trị nào của tham số m thì phương trình (2+√3)^x+(2-√3)^x=m có hai nghiệm phân biệt?

A. m > 2.        B. m < 2.        C.m=2.        D. m ≤ 2.

Lời giải:

Đáp án : A

Giải thích :

Nhận xét: (2+√3)(2-√3)=1 ⇔ (2+√3)^x (2-√3)^x=1.

Bảng biến thiên:

Dựa vào bảng biến thiên:

Nếu m > 2 thì phương trình (1')có hai nghiệm phân biệt ⇒ pt(1)có hai nghiệm phân biệt.

Bài 16: Với giá trị nào của tham số m thì phương trình 4^x-m.2^x+1+2m=0 có hai nghiệm x₁,x₂ thoả mãn x₁+x₂=3?

A. m=4.        B. m=2.        C. m=1.        D. m=3.

Lời giải:

Đáp án : D

Giải thích :

Ta có: 4^x-m.2^x+1 + 2m = 0 ⇔ (2^x)² - 2m.2^x+2m = 0(*)

Phương trình (*) là phương trình bậc hai ẩn 2^x có: Δ'=(-m)²-2m = m²-2m.

Phương trình (*) có nghiệm ⇔ m²-2m ≥ 0 ⇔ m(m-2) ≥ 0

Áp dụng định lý Vi-ét ta có: 2^x₁.2^x₂ = 2m ⇔ 2^x₁+x₂ = 2m

Do đó x₁+x₂=3 ⇔ 2³ = 2m ⇔ m = 4.

Thử lại ta được m=4 thỏa mãn. Chọn D.