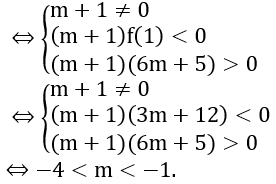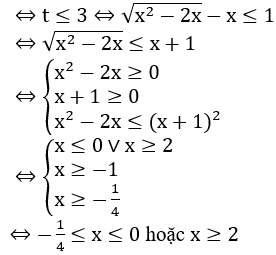Phương pháp giải bất phương trình mũ cực hay - Toán lớp 12

---

Phương pháp giải bất phương trình mũ cực hay

Với Phương pháp giải bất phương trình mũ cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải bất phương trình mũ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Bất phương trình mũ cơ bản có dạng a^x > b (hoặc a^x ≥ b, a^x < b, a^x ≤ b) với a > 0, a ≠ 1.

Ta xét bất phương trình có dạng a^x > b.

    • Nếu b ≤ 0, tập nghiệm của bất phương trình là R, vì a^x > b, ∀x ∈ R..

    • Nếu b > 0 thì bất phương trình tương đương với a^x > a^log_ab.

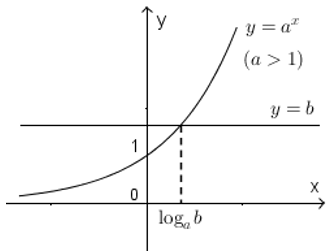
Với a > 1, nghiệm của bất phương trình là x > log_a b.

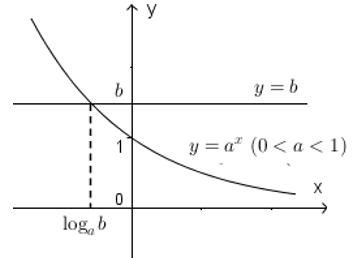
Với 0 < a < 1, nghiệm của bất phương trình là x < log_a b.

Ta minh họa bằng đồ thị sau:

    • Với a > 1, ta có đồ thị sau.

    • Với 0 < a < 1, ta có đồ thị sau.

Lưu ý:

1. Dạng 1:

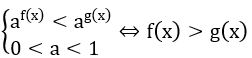
2. Dạng 2:

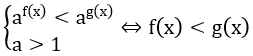
3. Dạng 3: a^f(x) > b(*)

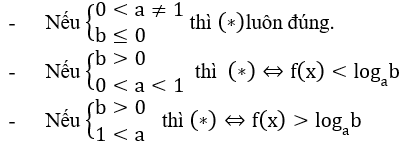
4. Dạng 4: a^f(x) < b(**)

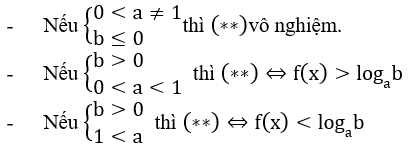
Lưu ý: Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.

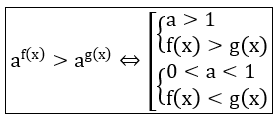
Tương tự với bất phương trình dạng:

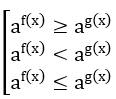
Trong trường hợp cơ số a có chứa ẩn số thì:

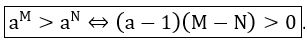
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:

    + Đưa về cùng cơ số.

    + Đặt ẩn phụ.

    + Sử dụng tính đơn điệu:

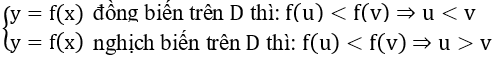
Ví dụ minh họa

Bài 1: Giải bất phương trình sau

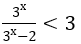
Hướng dẫn:

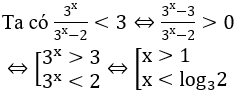
Bài 2: Giải bất phương trình sau 9^x-1-36.3^x-3+3 ≤ 0

Hướng dẫn:

Biến đổi bất phương trình (1) ta được

(1) ⇔ (3^x-1)²-4.3^x-1+3 ≤ 0 (2)

Đặt t = 3^x-1 (t > 0), bất phương trình (2) trở thành t²-4t+3 ≤ 0 (3)

(3) ⇔ 1 ≤ t ≤ 3

Suy ra: 1 ≤ 3^x-1 ≤ 3 ⇔ 0 ≤ x-1 ≤ 1 ⇔ 1 ≤ x ≤ 2

Vậy tập nghiệm của bất phương trình là S = [1;2]

Bài 3: Giải bất phương trình sau

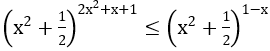
Hướng dẫn:

Vì x²+1/2 > 0 nên ta có các trường hợp sau

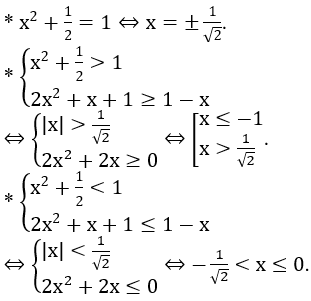
Vậy nghiệm của bất phương trình là:

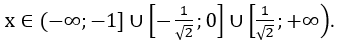
B. Bài tập vận dụng

Bài 1: Giải bất phương trình sau:

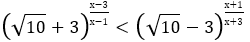
Lời giải:

Ta có (√10+3)(√10-3)=1 ⇒ √10-3 = (√10+3)^-1

Bất phương trình cho

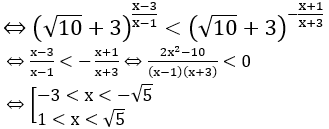
Bài 2: Giải bất phương trình sau:

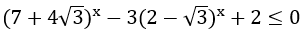
Lời giải:

Ta có: 7+4√3 = (2+√3)² và (2-√3)(2+√3) = 1 nên đặt

t = (2+√3)^x, t > 0 ta có bất phương trình:

t²-3/t+2 ≤ 0 ⇔ t³+2t-3 ≤ 0 ⇔ (t-1)(t²+t+3) ≤ 0 ⇔ t ≤ 1

⇔ (2+√3)^x ≤ 1 ⇔ x ≤ 0.

Vậy, bất phương trình cho có nghiệm là x ≤ 0

Bài 3: Giải bất phương trình sau:

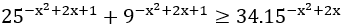
Lời giải:

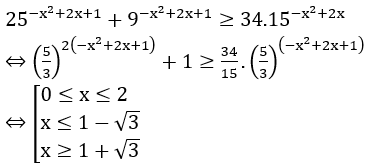
Bài 4: Giải bất phương trình sau:

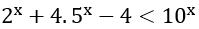
Lời giải:

Ta có 2^x + 4.5^x - 4 < 10^x ⇔ 2^x - 10^x + 4.5^x-4 < 0 ⇔ 2^x (1-5^x) - 4(1-5^x) < 0 ⇔ (1-5^x)(2^x-4) < 0

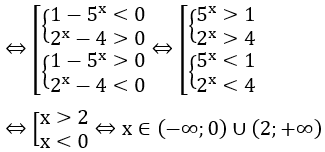
Bài 5: Giải bất phương trình sau:

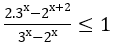
Lời giải:

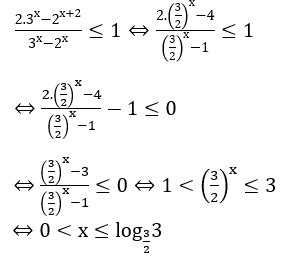
Bài 6: Giải bất phương trình sau:

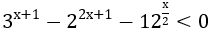
Lời giải:

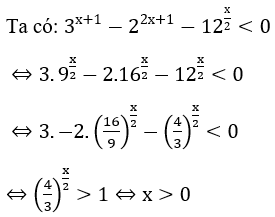
Bài 7: Giải bất phương trình sau:

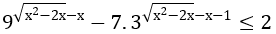
Lời giải:

Vậy bất phương trình cho có nghiệm là -1/4 ≤ x ≤ 0 hoặc x ≥ 2

Bài 8: Với giá trị nào của tham số m thì phương trình (m+1)16^x-2(2m-3) 4^x+6m+5=0 có hai nghiệm trái dấu.

Lời giải:

Đặt 4^x = t > 0. Phương trình đã cho trở thành:

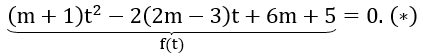
Yêu cầu bài toán ⇔ (*) có hai nghiệm t₁, t₂ thỏa mãn 0 < t₁ < 1 < t₂