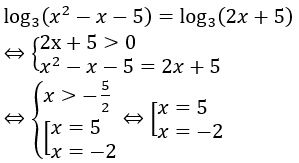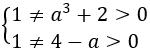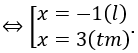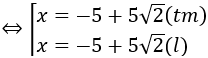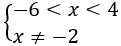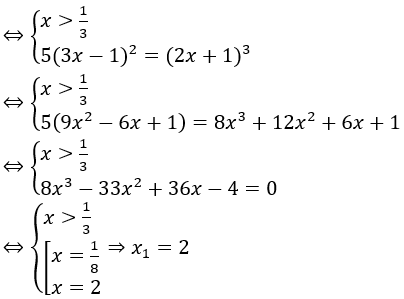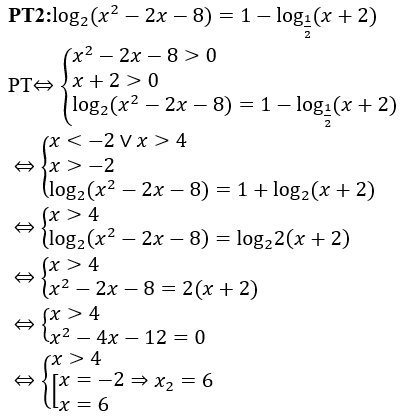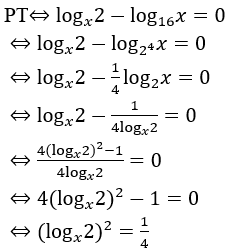Trắc nghiệm giải phương trình logarit bằng cách đưa về cùng cơ số - Toán lớp 12

---

Trắc nghiệm giải phương trình logarit bằng cách đưa về cùng cơ số

Với Trắc nghiệm giải phương trình logarit bằng cách đưa về cùng cơ số Toán lớp 12 tổng hợp 18 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình logarit bằng cách đưa về cùng cơ số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Tổng các nghiệm không âm của phương trình log_√3 x - log₃ (2x²-4x+3)=0 là:

A.1        B. 2        C.3        D. 4

Lời giải:

Đáp án : D

Giải thích :

Điều kiện x > 0

log_√3 x - log₃ (2x²-4x+3)=0 ⇔ 2log₃ x - log₃ (2x²-4x+3)=0 ⇔ log₃ x² = log₃ (2x²-4x+3) ⇔ x²=2x²-4x+3 ⇔ x²-4x+3=0

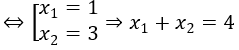
Bài 2: Cho phương trình log_a (x²+3x) = log_√a 2x , (a > 0;a ≠ 1), số nghiệm của phương trình trên là ?

A. 1.        B. 2        C. 3        D. 4

Lời giải:

Đáp án : A

Giải thích :

Điều kiện x > 0

log_a (x²+3x)=log_√a 2x ⇔ log_a (x²+3x)=2log_a 2x ⇔ log_a (x²+3x)=log_a 4x² ⇔ x²+3x=4x²

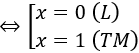
Vậy phương trình có một nghiệm.

Bài 3: Phương trình log_(a³+2) 3- log_(4-a) 3 = 0 có bao nhiêu nghiệm trên R?

A.0        B.1        C.2        D.3

Lời giải:

Đáp án : B

Giải thích :

Điều kiện

log_a³+2 3-log_4-a 3=0

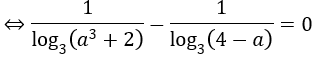
⇔ log₃ (a³+2)=log₃ (4-a) ⇔ a³+2=4-a ⇔ a³+a-2=0 ⇔ a=1 (TM)

Bài 4: Một học sinh giải phương trình log²₂ x - log₂ x² + 1 = 0 theo các bước như sau:

Bước 1: Điều kiện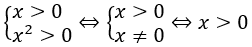

Bước 2: Từ điều kiện trên phương trình đã cho trở thành: (log₂ x)² - 2log₂ x + 1 = 0 ⇔ (log₂ x-1)² = 0 ⇔ log₂ x=1

Bước 3: Vậy nghiệm phương trình là x = 2¹ = 2 (nhận)

Bài trên sai ở bước nào?

A. Bước 1.        B. Bước 2.        C. Bước 3.        D. Không sai bước nào.

Lời giải:

Đáp án : D

Bài 5: Tập nghiệm của phương trình log₄ (x+2)=log₂ x là

A.S={2;-1}.        B.S={2}.        C.S={4}        D.S={4;-1}.

Lời giải:

Đáp án : B

Giải thích :

• Tự luận:

ĐK: x > 0.

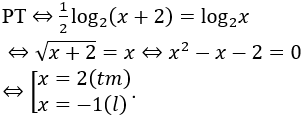
• Trắc nghiệm Đk x > 0 → Loại ngay đáp án A,D. Thử trực tiếp x=2 vào thấy thỏa mãn

Bài 6: Giải phương trình log₃ x+log₃ (x+2)=1.

A.x=3.        B.x=3∧x=-1.        C.x=(-1)/2.        D.x=6∧x=3.

Lời giải:

Đáp án : A

Giải thích :

• Tự luận: ĐK: x > 0.

PT ⇔ log₃ [x(x+2)] = log₃ 3 ⇔ x(x+2) = 3 ⇔ x²+2x-3 = 0

• Trắc nghiệm Đk x > 0 → Loại ngay đáp án B,C. Thử trực tiếp x=3 vào thấy thỏa mãn, x=6 thấy không thỏa mãn

Bài 7: Tập nghiệm của phương trình là

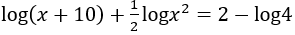
A.S={-5;-5+5√2}.        B. S={-5;-5-5√2}.

C.S={-5;-5-5√2;-5+5√2}.        D.S={-5-5√2;-5+5√2}.

Lời giải:

Đáp án : A

Giải thích :

• Tự luận: Đk x > -10.

PT ⇔ log(x+10) + log|x| = log100 - log4 ⇔ (x+10)|x| = 25.

TH1: x ≥ 0 ⇒ x²+10x-25=0

TH2: -10 < x < 0 ⇒ x²+10x+25 = 0 ⇔ x = -5 (tm).

Bài 8: Tập nghiệm của phương trình log_(2+√3) (x+1) = log_(2-√3) (x+2) là

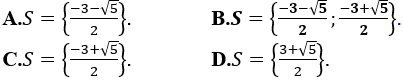
Lời giải:

Đáp án : C

Giải thích :

• Tự luận: Đk x > -1.

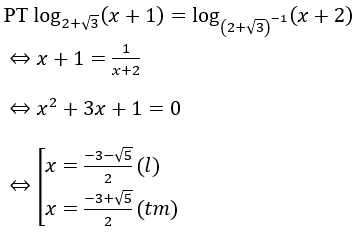
Bài 9:Tập nghiệm của phương trình

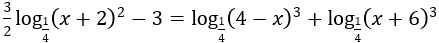
A.S={2}.        B.S={1-√33}.        C.S={2;1+√33}.        D.S={2;1-√33}.

Lời giải:

Đáp án : D

Giải thích :

• Tự luận: Đk

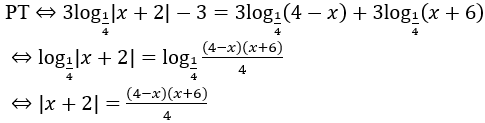
Th1.

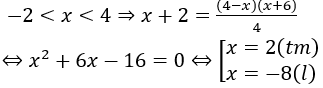
Th2.

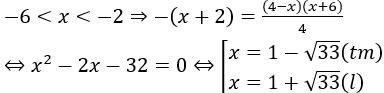
Bài 10: Số nghiệm của phương trình: log₄ x²=log_√2 2có được là:

A. 0.        B. 1.        C. 2.        D. 3.

Lời giải:

Đáp án : C

Giải thích :

ĐK: x² > 0 ⇔ x ≠ 0.

log₄ x² = log_√2 2 ⇔ log₂ |x| = log₂ 4 ⇔ |x| = 4 ⇔ x = ±4.

Bài 11: Số nghiệm của phương trình log₄ (log₂ x)+log₂ (log₄ x)=2 là:

A. 0.        B. 2.        C. 3.        D. 1.

Lời giải:

Đáp án : D

Giải thích :

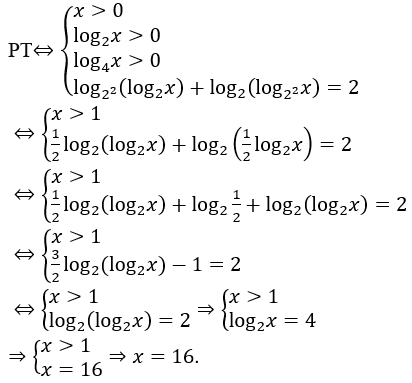
Bài 12: Số nghiệm của phương trình log₂ (x³+1)-log₂ (x²-x+1)-2log₂ x=0 là:

A. 0.        B. 2.        C. 3.        D. 1.

Lời giải:

Đáp án : A

Giải thích :

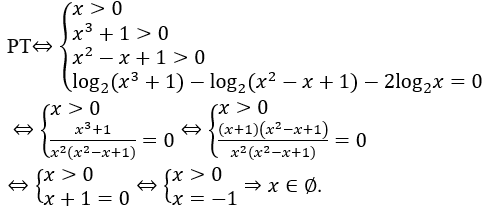
Bài 13: Số nghiệm của phương trình log₅ (5x)-log₂5 (5x)-3=0 là :

A. 3.        B. 4.        C. 1.        D. 2.

Lời giải:

Đáp án : A

Giải thích :

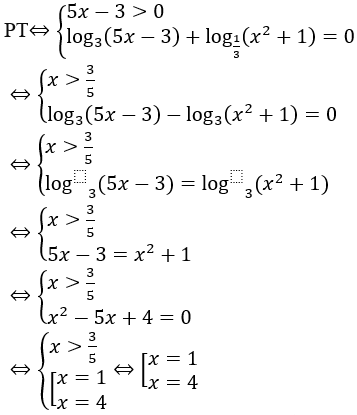
Bài 14: Phương trình log₃ (5x-3)+log_(1/3) (x²+1)=0 có 2 nghiệm x₁, x₂ trong đó x₁ < x₂.Giá trị của P=2x₁+3x₂ là

A. 5.        B. 14.        C. 3.        D. 13.

Lời giải:

Đáp án : B

Giải thích :

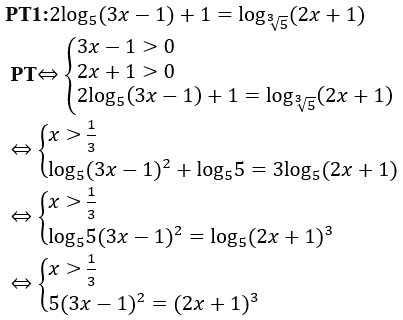
Vậy 2x₁+3x₂=2.1+3.4=14.

Bài 15: Hai phương trình 2log₅ (3x-1)+1=log_∛5 (2x+1) và log₂ (x²-2x-8)=1-log_(1/2) (x+2) lần lượt có 2 nghiệm duy nhất là x₁,x₂. Tổng x₁+x₂ là?

A. 8.        B. 6.        C. 4.        D. 10.

Lời giải:

Đáp án : A

Giải thích :

Vậy x₁+x₂=2+6=8.

Bài 16: Gọi x₁, x₂ là nghiệm của phương trình log_x 2-log₁₆ x = 0. Khi đó tích x₁.x₂bằng:

A. -1.        B. 1.        C. 2.        D. -2.

Lời giải:

Đáp án : B

Giải thích :

[Phương pháp tự luận]

Điều kiện: 0 < x ≠ 1

[Phương pháp trắc nghiệm]

Đáp án B, D có tích âm thì có thể x₁ < 0 hoặc x₂ < 0 thì không thỏa mãn điều kiện của x nên loại.

Bài 17: Số nghiệm của phương trình ln(x²-6x+7)=ln(x-3)là:

A. 0.        B. 2.        C. 3.        D. 1.

Lời giải:

Đáp án : D

Giải thích :

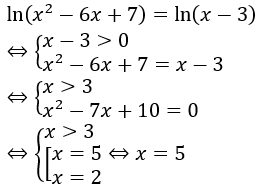
Bài 18: Gọi x₁,x₂là 2 nghiệm của phương trình log₃ (x²-x-5) = log₃ (2x+5). Khi đó |x₁-x₂ | bằng:

A. 5.        B. 3.        C. -2.        D. 7.

Lời giải:

Đáp án : D

Giải thích :