Tìm cực trị của hàm số dựa vào đồ thị cực hay, có lời giải - Toán lớp 12
Tìm cực trị của hàm số dựa vào đồ thị cực hay, có lời giải
Với Tìm cực trị của hàm số dựa vào đồ thị cực hay, có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm cực trị của hàm số dựa vào đồ thị từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải
- Bước 1: Lập bảng biến của hàm số y = f(x) dựa vào đồ thị hàm y = f'(x)
Nếu đồ thị hàm số y = f'(x) nằm bên dưới trục hoành thì f'(x) mang dấu âm
Nếu đồ thị hàm số y = f'(x) nằm bên trên trục hoành thì f'(x) mang dấu dương
- Bước 2: Dựa vào bảng biến thiên để kết luận về điểm cực trị của hàm số
Hàm số y = f(x) có đạo hàm đổi dấu từ âm sang dương tại x = x0 thì hàm số đạt cực tiểu tại x = x0
Hàm số y = f(x) có đạo hàm đổi dấu từ dương sang âm tại x = x0 thì hàm số đạt cực đại tại x = x0
Chú ý: Nếu hàm số y = f'(x) cắt trục hoành tại x0 thì f'(x) đổi dấu khi qua x0
Nếu hàm số y = f'(x) tiếp xúc với trục hoành tại x0 thì f'(x) không đổi dấu khi qua x0
B. Ví dụ minh họa
Ví dụ 1: Cho hàm số y = f(x) xác định và có đạo hàm f'(x). Biết rằng hình vẽ bên là đồ thị của hàm số y = f'(x). Khẳng định nào sau đây là đúng về cực trị của hàm số y = f(x).
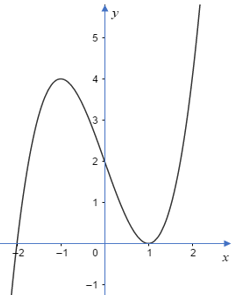
Lời giải
Chọn D
Từ đồ thị của hàm số y = f'(x), ta suy ra BBT:
Vậy hàm số y = f(x) đạt cực tiểu tại x = -2.
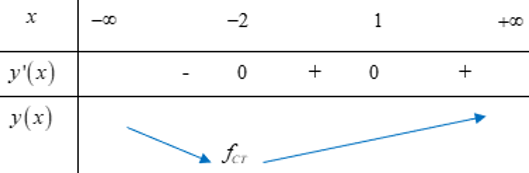
Ví dụ 2: Cho hàm số y = f(x) xác định và có đạo hàm f'(x). Đồ thị của hàm số g = f'(x) có đồ thị
Điểm cực đại của hàm số là
A. x = 4.
B. x = 3.
C. x = 1.
D. x = 2.
Lời giải
Chọn D
Từ đồ thị của hàm số g = f'(x), ta suy ra BBT:
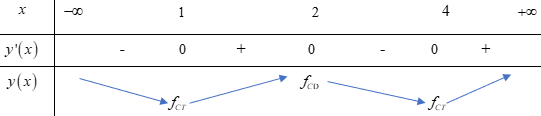
Dựa vào BBT ta thấy hàm số đã cho đạt cực đại tại x = 2.
Ví dụ 3: Cho hàm số y = f(x) có có đồ thị của hàm số y = f'(x) như hình vẽ bên.
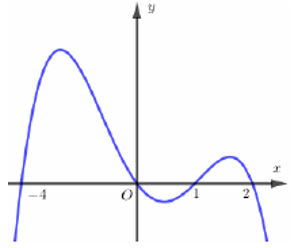
Hàm số y = f(x) có bao nhiêu điểm cực trị
A. 3.
B. 2.
C. 1.
D. 4.
Lời giải
Chọn D
Bảng biến thiên:
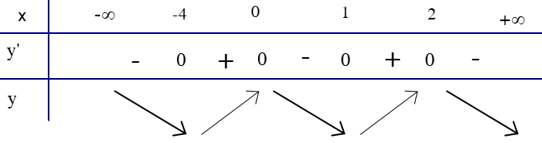
Suy ra hàm số có 4 điểm cực trị.
C. Bài tập trắc nghiệm
Bài 1: Cho hàm số y = f(x) có đạo hàm trên R. Hàm số y = f'(x) có đồ thị như hình vẽ bên
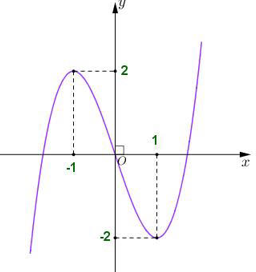
Giá trị cực đại của hàm số đã cho bằng
A. f(0).
B. f(1).
C. f(2).
D. f(-1).
Lời giải:
Chọn D
Dựa vào đồ thị hàm số, hàm số đã cho đạt cực đại tại x = -1 và đạt cực tiểu tại x = 1.
Do đó giá trị cực đại của hàm số đã cho là f(-1).
Bài 2: Cho hàm số y = f(x) có đạo hàm trên R và đồ thị hàm số y = f'(x) như hình vẽ:
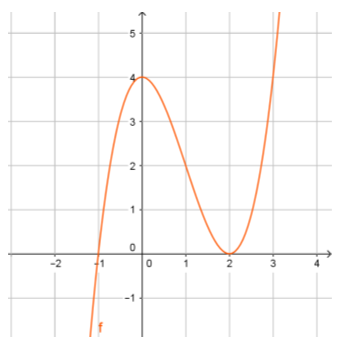
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
A. 3.
B. 1.
C. 2.
D. 0.
Lời giải::
Chọn B
Ta thấy f'(x) chỉ đổi dấu khi đi qua x = -1 nên đồ thị hàm số có duy nhất 1 điểm cực trị
Bài 3: Cho hàm số y = f(x) xác định trên R và có đồ thị hàm số y = f'(x) là đường cong trong hình dưới.
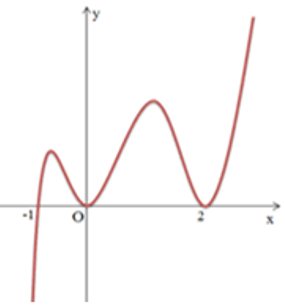
Mệnh đề nào dưới đây đúng?
A. Hàm số y = f(x) đạt cực tiểu tại x = 2 và x = 0 .
B. Hàm số y = f(x) có 4 cực trị.
C. Hàm số y = f(x) đạt cực tiểu tại x = -1.
D. Hàm số y = f(x) đạt cực đại tại x = -1.
Lời giải:
Chọn C
Giá trị của hàm số y = f'(x) đổi dấu từ âm sang dương khi qua x = -1 nên hàm số đạt cực tiểu tại x = -1
Bài 4: Hàm số y = f(x) có đạo hàm f'(x) trên khoảng K như hình vẽ bên dưới.
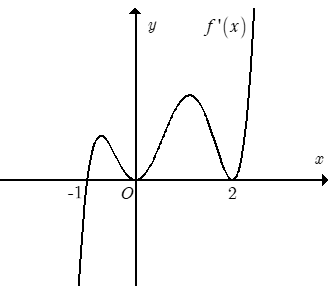
Hỏi hàm số f(x) có bao nhiêu điểm cực trị?
A. 0.
B. 1.
C. 2.
D. 4.
Lời giải:
Chọn B
Đồ thị hàm số f'(x) cắt trục hoành tại 1 điểm duy nhất (không tính tiếp xúc) có nghĩa là đạo hàm chỉ đổi dấu một lần nên hàm số có 1 điểm cực trị.
Bài 5: Hàm số y = f(x) liên tục trên khoảng R, biết đồ thị của hàm số y = f'(x) trên Knhư hình vẽ bên.
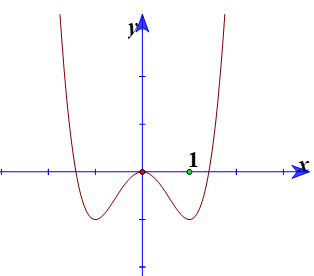
Tìm số cực trị của hàm số y = f(x) trên R.
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải::
Chọn B
Ta thấy đồ thị hàm số f'(x) cắt trục hoành tại 2 điểm nên đạo hàm đổi dấu tại đây và tiếp xúc với trục hoành tại x = 0 nên đạo hàm không đổi dấu. Do đó hàm số y = f(x) có 2 điểm cực trị.
Bài 6: Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ
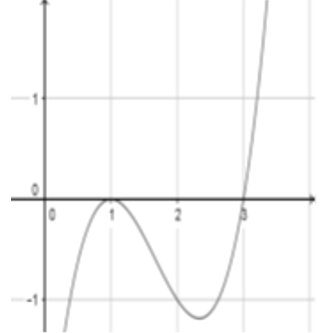
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số y = f(x) đạt cực đại tại x = 1 .
B. Hàm số y = f(x) có một điểm cực tiểu.
C. Đồ thị hàm số y = f(x) có hai điểm cực trị.
D. Hàm số không có cực trị.
Lời giải:.
Chọn B
Dựa vào đồ thị của y = f'(x) ta có bảng xét dấu
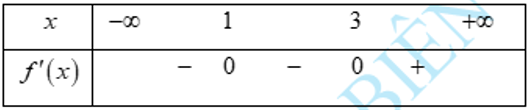
Dựa vào bảng xét dấu hàm số đạt cực tiểu tại x = 3.
Bài 7: Cho hàm số y = f(x) có đạo hàm trên R và đồ thị hàm số y = f'(x) trên R như hình bên dưới. Khi đó trên R hàm số y = f(x)
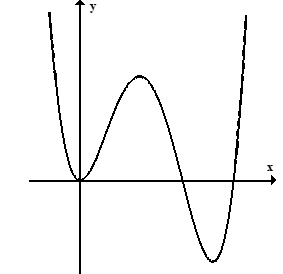
A. Có 1 điểm cực đại và 1 điểm cực tiểu.
B. Có 2 điểm cực đại và 2 điểm cực tiểu.
C. Có 1 điểm cực đại và 2 điểm cực tiểu.
D. Có 2 điểm cực đại và 1 điểm cực tiểu.
Lời giải:.
Chọn A
Dựa vào đồ thị hàm số f'(x) ta có bảng xét dấu:

Ta thấy f'(x) đổi dấu từ dương sang âm khi đi qua x1 và đổi dấu từ âm sang dương khi đi qua x2. Vậy hàm số y = f(x) có 1 cực đại và một cực tiểu.
Bài 8: Cho hàm số y = f(x) có đạo hàm trên R và đồ thị hàm f'(x) như hình vẽ
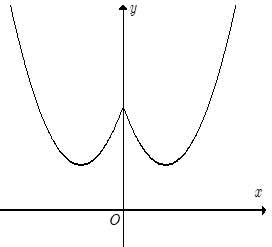
Hàm số y = f(x) đã cho có bao nhiêu điểm cực tiểu
A. 3.
B. 0.
C. 1.
D. 2.
Lời giải:
Chọn B
Dựa vào đồ thị ta thấy f'(x) > 0, ∀ x ∈ R nên hàm số y = f(x) đồng biến trên R
Vậy hàm số y = f(x) không có cực trị
Bài 9: Cho hàm số y = f(x) có có đồ thị của hàm số y = f'(x) như hình vẽ bên. Hàm số y = f(x2)có bao nhiêu điểm cực tiểu
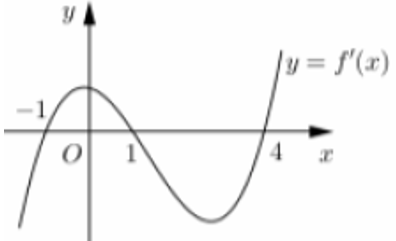
A. 3.
B. 2.
C. 1.
D. 4.
Lời giải:
Chọn A
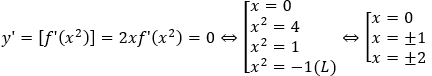
Bảng biến thiên:

Hàm số có ba điểm cực tiểu.
Bài 10: Cho hàm số y = f(x) có đồ thị đạo hàm y = f'(x) như hình bên.
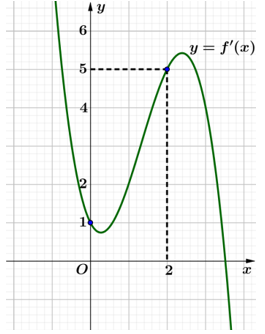
Khẳng định nào sau đây là đúng?
A. Hàm số y = f(x) - x2 - x đạt cực đại tại x = 0.
B. Hàm số y = f(x) - x2 - x đạt cực tiểu tại x = 0.
C. Hàm số y = f(x) - x2 - x không đạt cực trị tại x = 0.
D. Hàm số y = f(x) - x2 - x không có cực trị.
Lời giải:
Chọn A
Ta có: y' = f'(x) - (2x + 1)Þy' = 0 ⇔ f'(x) = 2x + 1.
Từ đồ thị ta thấy x = 0 là nghiệm đơn của phương trình y' = 0.
Ta có bảng biến thiên trên (-∞;2):
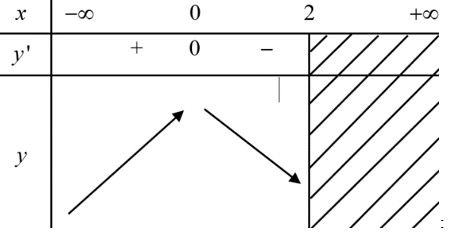
Từ bảng biến thiên Þ hàm số đạt cực đại tại x = 0.

