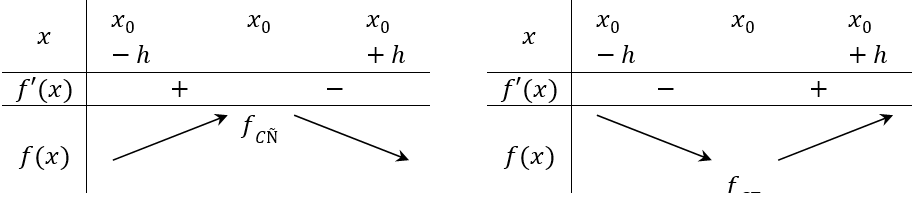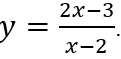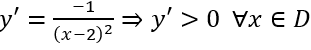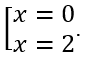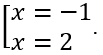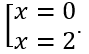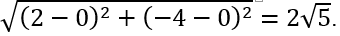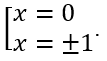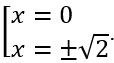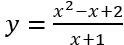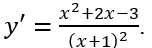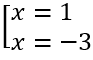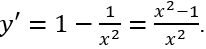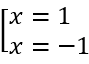Cách tìm cực trị của hàm số cực hay - Toán lớp 12

---

Cách tìm cực trị của hàm số cực hay

Với Cách tìm cực trị của hàm số cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm cực trị của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Phương pháp giải

1.Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x₀∈(a;b).

Nếu tồn tại số h > 0 sao cho f(x)< f(x₀ ) với mọi x ∈ (x₀ - h;x₀ + h) và x≠x_0 thì ta nói hàm số f_(x) đạt cực đại tại x₀.

Nếu tồn tại số h >0 sao cho f(x) >f(x₀ ) với mọi x ∈ (x₀ - h;x₀ + h) và x ≠ x₀ thì ta nói hàm số f_(x) đạt cực tiểu tại x₀.

2.Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên

K=(x₀ - h;x₀ + h)và có đạo hàm trên K hoặc trên K\{x₀}, với h >0.

Nếu f'(x)> 0 trên khoảng (x₀ - h;x₀) và f'(x) <0 trên (x₀;x₀ + h) thì x₀ là một điểm cực đại của hàm số f(x).

Nếu f'(x) < 0 trên khoảng (x₀ - h;x₀) và f'(x) >0 trên (x₀;x₀+ h) thì x₀ là một điểm cực tiểu của hàm số f(x).

Minh họa bằng bảng biến thiến

Chú ý.

Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là f_CÑ (f_CT), còn điểm M(x₀;f(x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3.Quy tắc tìm cực trị của hàm số

Quy tắc 1:

   Bước 1. Tìm tập xác định của hàm số.

   Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.

   Bước 3. Lập bảng biến thiên.

   Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2:

   Bước 1. Tìm tập xác định của hàm số.

   Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệux_i (i=1,2,3,...)là các nghiệm của nó.

   Bước 3. Tính f''(x) và f''(x_i ) .

   Bước 4. Dựa vào dấu của f''(x_i )suy ra tính chất cực trị của điểm x_i.

Ví dụ minh họa

Ví dụ 1. Tìm cực trị của hàm số y = 2x³ - 6x + 2.

Hướng dẫn

Tập xác định D = R.

Tính y' = 6x² - 6. Cho y'= 0 ⇔ 6x² - 6 = 0 ⇔ x = ±1.

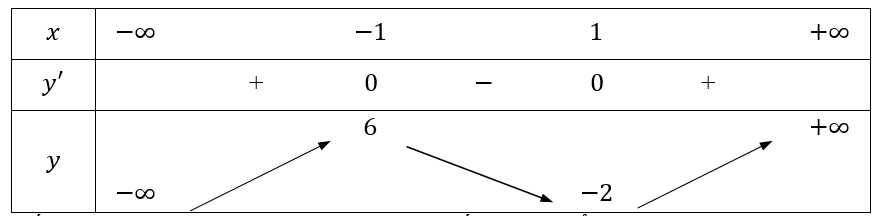
Bảng biến thiên

Vậy hàm số đạt cực đại tại x = - 1, y = 6 và hàm số đạt cực tiểu tại x = 1,y = -2.

Ví dụ 2. Tìm cực trị của hàm số y = x⁴ - 2x² + 2.

Hướng dẫn

Tập xác định D = R.

Tính y' = 4x³ - 4x. Cho y'= 0 ⇔ 4x³ - 4x = 0 ⇔.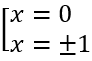

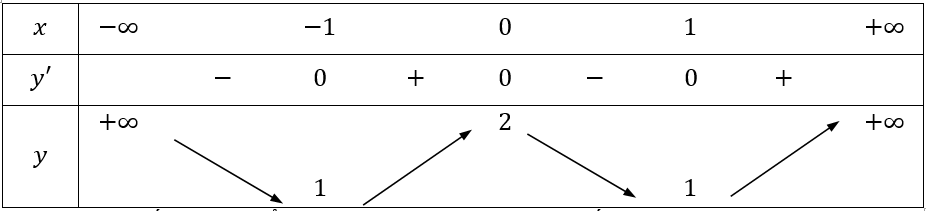
Bảng biến thiên

Vậy hàm số đạt cực tiểu tại x = ±1, y = 1 và hàm số đạt cực đại tại x = 0, y = 2.

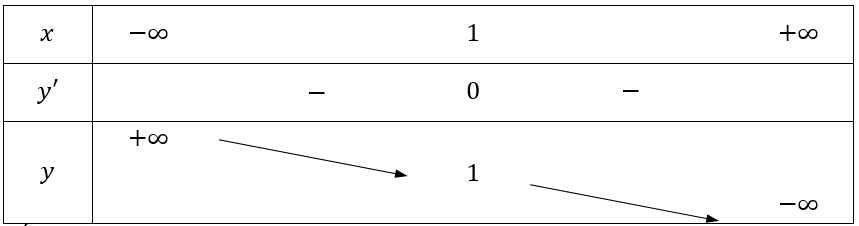
Ví dụ 3. Tìm cực trị của hàm số y =

Hướng dẫn

Tập xác định D = R\{2}. Tính

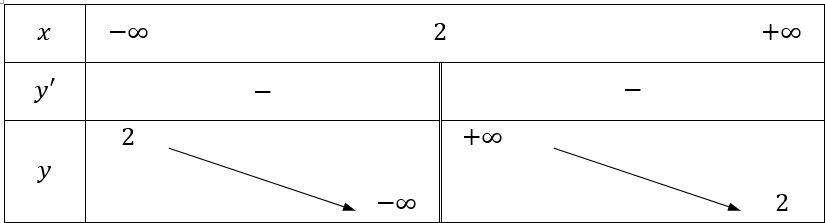
Bảng biến thiên

Vậy hàm số đã cho không có cực trị.

B. Bài tập vận dụng

Bài 1. Tìm cực trị của hàm số y = -x³ + 3x² - 4

Lời giải:

Tập xác định D = R.

Tính y'= -3x² + 6x.

Cho y'= 0⇔-3x² + 6x = 0⇔

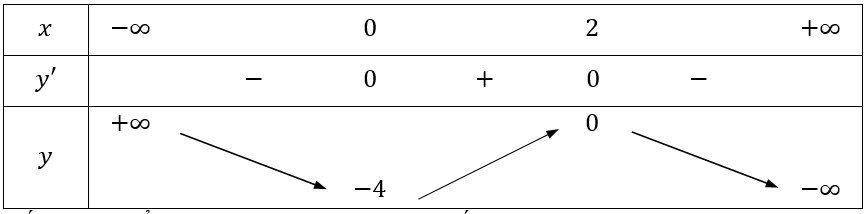
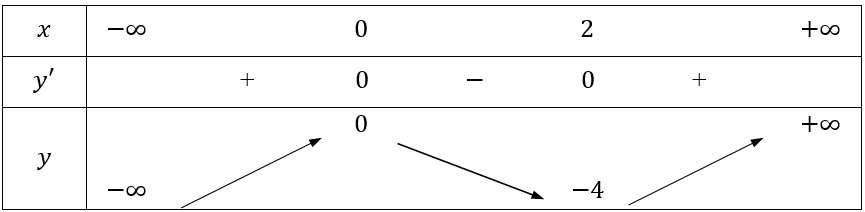
Bảng biến thiên

Vậy hàm số đạt cực tiểu tại x = 0,y = -4 và hàm số đạt cực đại tại x = 2,y = 0.

Bài 2. Tìm cực trị của hàm số y = -x³ + 3x³ - 3x + 2

Lời giải:

Tập xác định D = R.

Tính y' = -3x² + 6x-3.

Cho y'= 0 ⇔ -3x²+ 6x-3 = 0 ⇔ x = 1.

Bảng biến thiên

Vậy hàm số đã cho không có cực trị.

Bài 3. Gọi A,B là hai điểm cực trị của đồ thị hàm số y = 2x³ - 3x² - 12x + 1. Tìm tọa độ A,B và phương trình đường thẳng qua hai điểm đó.

Lời giải:

Tập xác định D = R.

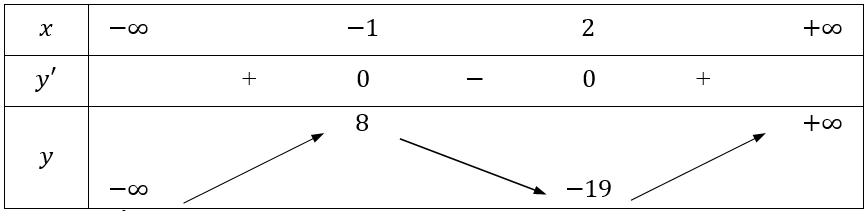
Tính y' = 6x² - 6x - 12.

Cho y'= 0 ⇔

Bảng biến thiên

Suy ra tọa độ hai điểm cực trị là A(-1;8), B(2;-19).

Vậy phương trình đường thẳng AB là 9x + y + 1 = 0.

Bài 4. Cho hàm số y = x³ - 3x² có đồ thị (C). Tìm các điểm cực đại, cực tiểu của đồ thị (C)và khoảng cách giữa hai điểm cực trị đó.

Lời giải:

Tập xác định D = R.

Tính y'= 3x²-6x.

Cho y'= 0 ⇔

Bảng biến thiên

Vậy tọa độ hai điểm cực trị là A(-1;8),B(2;-19). Khi đó AB =

Bài 5. Tìm cực trị của hàm số y = x⁴/4 - x² + 2

Lời giải:

Tập xác định D = R.

Tính y'= 2x³-2x.

Cho y'= 0 ⇔ 4x³ - 4x = 0 ⇔

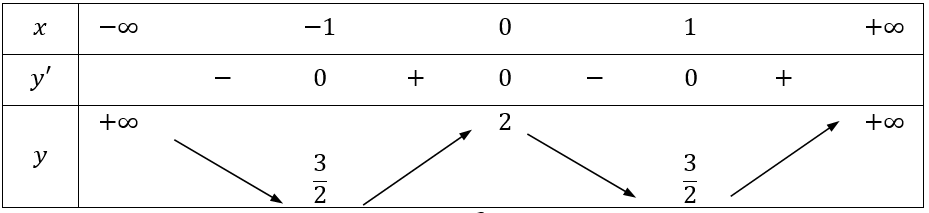
Bảng biến thiên

Vậy hàm số đạt cực tiểu tại x = ±1, y = 3/2 và hàm số đạt cực đại tại x = 0, y = 2.

Bài 6. Tìm cực trị của hàm số y = -x⁴ + 4x² - 5

Lời giải:

Tập xác định D = R.

Tính y'= -4x³ + 8x.

Cho y'= 0 ⇔ -4x³ + 8x = 0⇔

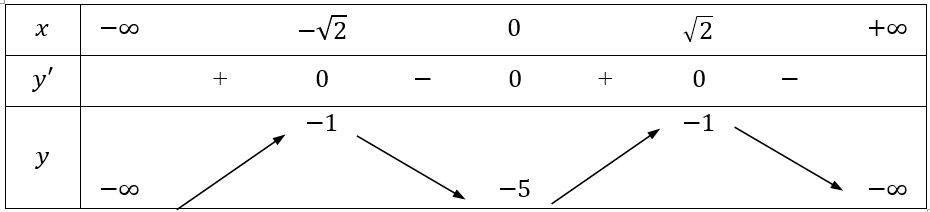
Bảng biến thiên

Vậy hàm số đạt cực tiểu tại x = 0, y = -5 và hàm số đạt cực đại tại x = ±√2, y = -1.

Bài 7. Tìm cực trị của hàm số y =

Lời giải:

Tập xác định D = R\{-1}.

Tính y' =

Cho y' = 0⇔ x² + 2x - 3 = 0 ⇔

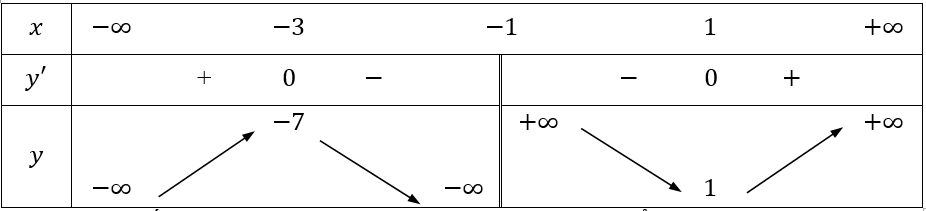
Bảng biến thiên

Vậy hàm số đạt cực đại tại x = -3, y = -7 và đạt cực tiểu tại x = 1, y = 1.

Bài 8. Tìm cực trị của hàm số y = x - 5 + 1/x

Lời giải:

Tập xác định D = R\{0}.

Tính

Cho y' = 0⇔x² - 1 = 0 ⇔

Bảng biến thiên

Vậy hàm số đạt cực đại tại x = -1, y = -7 và đạt cực tiểu tại x = 1, y = -3.