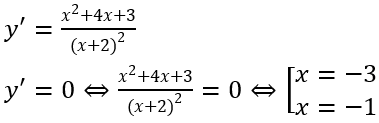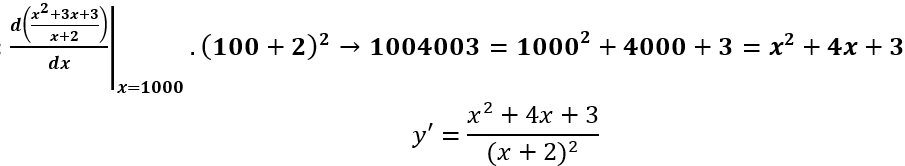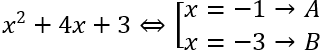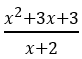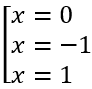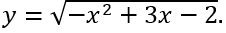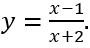Bài tập trắc nghiệm Tìm cực trị của hàm số cực hay - Toán lớp 12
Bài tập trắc nghiệm Tìm cực trị của hàm số cực hay
Với Bài tập trắc nghiệm Tìm cực trị của hàm số cực hay Toán lớp 12 tổng hợp 12 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm cực trị của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
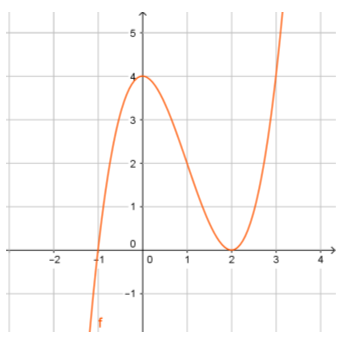
Câu 1: Cho hàm số y = f(x) có đồ thị như hình vẽ:
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
A. 2. B. 1. C. 0. D. 3.
Lời giải:
Đáp án : A
Câu 2: Cho hàm số y = x3 - 3x2 + 2 . Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 0.
B. Hàm số đạt cực tiểu tại x = 2 và đạt cực đại x = 0.
C. Hàm số đạt cực đại tại x = -2và cực tiểu tại x = 0.
D. Hàm số đạt cực đại tại x = 0và cực tiểu tại x = -2.
Lời giải:
Đáp án : B
Giải thích :
y' = 3x2 - 6x = 0 ⇔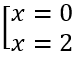 
Lập bảng biến thiên ta được hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 0
Câu 3: Cho hàm số y = x4 - 2x2 + 3 . Khẳng định nào sau đây là đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng 2 điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có đúng một điểm cực trị.
Lời giải:
Đáp án : A
Giải thích :
y' = 4x3 - 4x = 0 ⇔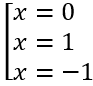
y(0) = 3; y(1) = y(-1) = 2 nên hàm số có hai cực trị.
Câu 4: Gọi M, n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số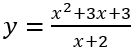 
. Khi đó giá trị của biểu thức M2 - 2n bằng:
A. 8. B. 7. C. 9. D. 6.
Lời giải:
Đáp án : B
Giải thích :
Hàm số đạt cực đại tại x = -3 và yCD = -3
Hàm số đạt cực tiểu tại x = -1 và yCT = 1
⇒ M2 - 2n = 7
Phương pháp trắc nghiệm:
Bấm máy tính:
Bước 1:
Bước 2: Giải phương trình bậc hai :
Bước 3: Nhập vào máy tính 
Caclx = A → C
Caclx = B → D
Bước 4: Tính C2 - 2D = 7
Câu 5: Cho hàm số y = x3 + 17x2 - 24x + 8 . Kết luận nào sau đây là đúng?
A. xCD = 1. B. xCD = 2/3. C. xCD = -3. D. xCD = -12.
Lời giải:
Đáp án : D
Giải thích :
y' = 3x2 + 34x - 24 = 0 ⇔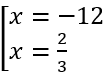 
Lập bảng biến thiên ta thấy hàm số đạt cực đại tại x = -12 .
Câu 6: Cho hàm số y = 3x4 - 6x2 + 1 . Kết luận nào sau đây là đúng?
A. yCD = -2. B. yCD = 1. C. yCD = -1. D. yCD = 2.
Lời giải:
Đáp án : B
Giải thích :
y' = 12x3 - 12x = 0 ⇔
Hàm số đạt cực đại tại x = 0 và yCD = 1 .
Câu 7: Trong các hàm số sau, hàm số nào đạt cực đại tại x = 3/2 ?
A.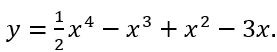 
B. 
C.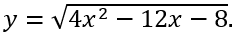 
D. 
Lời giải:
Đáp án : B
Giải thích :
Hàm số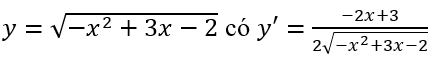 
và y' đổi dấu từ "+" sang "-" khi x chạy qua 3/2 nên hàm số đạt cực đại tại x = 3/2 .
Dùng casio kiểm tra: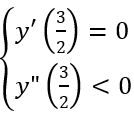 
thì hàm số đạt cực đại tại 3/2 .
Câu 8: Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu?
A. y = -10x4 - 5x2 + 7. B. y = -17x3 + 2x2 + x + 5.
C.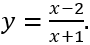 
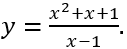
D. 
Lời giải:
Đáp án : A
Giải thích :
Hàm số y = -10x4 - 5x2 + 7 có y' = -40x3 - 10x = 0 ⇔ x = 0 và y"(0) = -10 < 0 nên hàm số đạt cực đại tại x = 0 .
Câu 9: Cho hàm số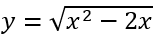 
. Khẳng định nào sau đây là đúng
A. Hàm số có hai điểm cực trị. B. Hàm số đạt cực tiểu tại x = 0 .
C. Hàm số đạt cực đại x = 2 . D. Hàm số không có cực trị.
Lời giải:
Đáp án : D
Giải thích :
TXĐ: D = (-∞;0]∪[2;+∞) .
⇔ x = 1(l) .
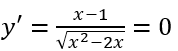
y' không đổi dấu trên các khoảng xác định nên hàm số không có cực trị.
Câu 10: Cho hàm số y = x7 - x5 . Khẳng định nào sau đây là đúng
A. Hàm số có đúng 1 điểm cực trị. B. Hàm số có đúng 3 điểm cực trị .
C. Hàm số có đúng hai điểm cực trị. D. Hàm số có đúng 4 điểm cực trị.
Lời giải:
Đáp án : C
Giải thích :
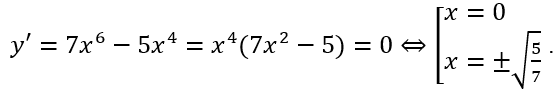
y' chỉ đổi dấu khi x chạy qua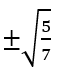 
nên hàm số có hai điểm cực trị.
Câu 11: Cho hàm số y = f(x) có đạo hàm f'(x) = (x+1)(x-2)2 (x-3)3 (x+5)4 . Hỏi hàm số
y = f(x) có mấy điểm cực trị?
A. 2. B. 3. C.4. D. 5.
Lời giải:
Đáp án : A
Giải thích :
f'(x) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.
Câu 12: Cho hàm số y = -x3 + 3x2 + 6x . Hàm số đạt cực trị tại hai điểm x_1,x_2 . Khi đó giá trị của
biểu thức S=x12 + x22 bằng:
A. -10. B.-8. C.10. D. 8.
Lời giải:
Đáp án : D
Giải thích :
D = R
y' = -3x2 + 6x + 6
Phương trình y' = 0 luôn có hai nghiệm phân biệt x1, x2 và y' đổi dấu khi x chạy qua x1,x2 nên hàm số đạt cực trị tại x1,x2.
S = x12 + x22 = (x1 + x2 )2 - 2x1 x2 = 8
Phương pháp trắc nghiệm:
Bước 1: Giải phương trình bậc hai : 
Bước 2: Tính A2 + B2 = 8
