Tìm m để hàm số có 3 điểm cực trị tạo thành tam giác có diện tích cực hay, có lời giải - Toán lớp 12

Tìm m để hàm số có 3 điểm cực trị tạo thành tam giác có diện tích cực hay, có lời giải

Với Tìm m để hàm số có 3 điểm cực trị tạo thành tam giác có diện tích cực hay, có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm m để hàm số có 3 điểm cực trị tạo thành tam giác có diện tích từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

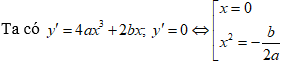
(C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt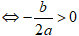

Đồ thị hàm số có 3 điểm cực trị là:

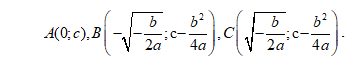
Tam giác ABC cân tại A, gọi H là trung điểm của BC thì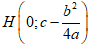

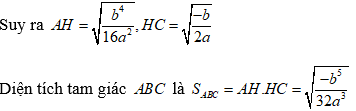
Chú ý: Đồ thị hàm trùng phương có 3 điểm cực trị lập thành 1 tam giác có diện tích S₀

⇔ 32a³ (S₀)² + b⁵ = 0

B. Ví dụ minh họa

Ví dụ 1: Tìm tất cả các giá trị thực của m để đồ thị hàm số y = x⁴ - mx² + 1 có ba điểm cực trị lập thành một tam giác có diện tích bằng 1.

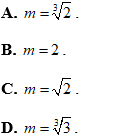
Lời giải

Chọn B

Cách 1:

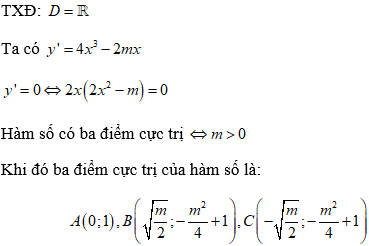
Tam giác ABC cân tại A, gọi H là trung điểm của BC thì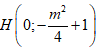

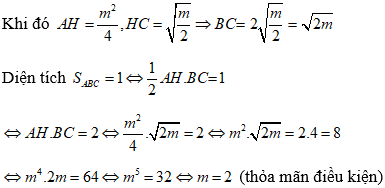
Cách 2:

Áp dụng công thức giải nhanh ta có đồ thị hàm số có 3 điểm cực trị lập thành tam giác có diện tích bằng 1 ⇔ 32.1³.1² + (-m)⁵ = 0 ⇔ m = 2

Ví dụ 2: Cho hàm số y = -x⁴ + 2(m - 2)x² + m² - 5m + 5. Tìm tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 1.

A. m = ±3.

B. m = 3.

C. m = 2.

D. m = ±2.

Lời giải

Chọn B

Cách 1:

Ta có: y' = -4x³ + 4(m - 2)x = -4x[x² - (m - 2)].

Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi phương trình y' = 0 có 3 nghiệm phân biệt

⇔ m - 2 > 0 ⇔ m > 2.

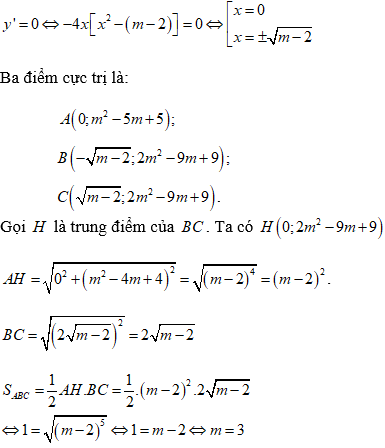
Vậy với m = 3 thì đồ thị hàm số đã cho có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 1.

Cách 2: Sử dụng công thức giải nhanh.

Đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 1 thì

32.(-1)³.1² + [2(m - 2)]⁵ = 0 ⇔ 1 = m - 2 ⇔ m = 3.

Ví dụ 3: Để đồ thị hàm số y = x⁴ - 2mx² + m - 1 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 2, giá trị của tham số m thuộc khoảng nào sau đây?

A. (2;3).

B. (-1;0).

C. (0;1).

D. (1;2).

Lời giải

Chọn D

Ví dụ 4: Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x⁴ - 2(1 - m²)x² + m + 1 có 3 điểm cực trị tạo thành tam giác có diện tích lớn nhất.

A. m = -1.

B. m = 0.

C. m = 1.

D. m = 2.

Lời giải

Chọn B

Ta có y' = 4x³ - 4(1 - m²)x.

Hàm số có 3 điểm cực trị ⇔ y' = 4x(x² - (1 - m²)) = 0 có 3 nghiệm phân biệt

⇔ -1 < m < 1.

Khi đó tọa độ 3 điểm cực trị của đồ thị hàm số là