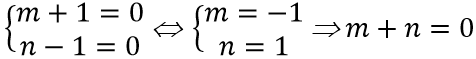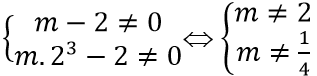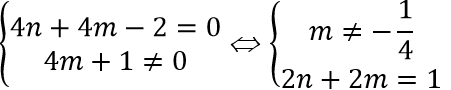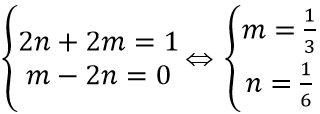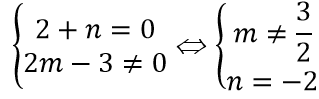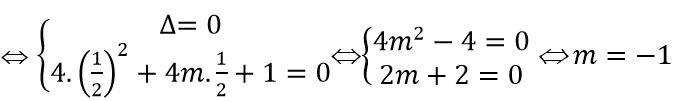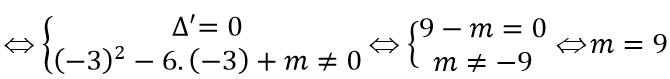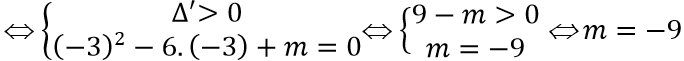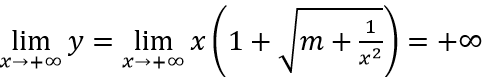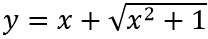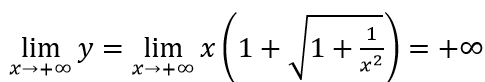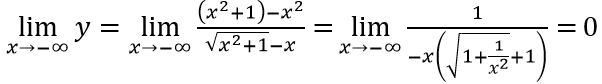Tìm tham số m để hàm số có tiệm cận cực hay - Toán lớp 12

Tìm tham số m để hàm số có tiệm cận cực hay

Với Tìm tham số m để hàm số có tiệm cận cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tham số m để hàm số có tiệm cận từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Ví dụ minh họa

Ví dụ 1.(THPT Chuyên Bảo Lộc – Lâm Đồng 2017). Cho hàm số 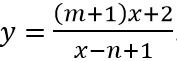. Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Tính giá trị biểu thức P = m + n.

Hướng dẫn

Đồ thị hàm số có tiệm cận ngang y = m + 1 và tiệm cận đứng x = n - 1. Do đó đồ thị hàm số nhận trục tung x = 0 và trục hoành y = 0 làm tiệm cận khi và chỉ khi

Ví dụ 2 (THPT chuyên Thái Nguyên 2017 L2). Tìm m để đồ thị hàm số 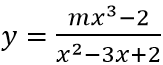có hai đường tiệm cận đứng.

Hướng dẫn

Ta có x² - 3x + 2 = 0 ⇔ x = 1 hoặc x = 2

Để hai đường thẳng x = 1 và x = 2 là đường tiệm cận của đồ thị hàm số thì x = 1 và x = 2 không là nghiệm của tử số mx³ - 2. Tức là:

Ví dụ 3: Tìm tất cả các giá trị của tham số m để đồ thị hàm số 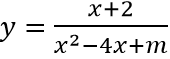có tiệm cận ngang mà không có tiệm cận đứng.

Hướng dẫn

Ta có 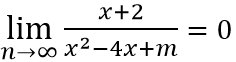nên y = 0 là tiệm cận ngang của đồ thị hàm số.

Do đó để đồ thị hàm số có tiệm cận ngang mà không có tiệm cận đứng thì

phương trình x² - 4x + m = 0 vô nghiệm ⇔ Δ' < 0 ⇔ 4 - m < 0 ⇔ m > 4

B. Bài tập vận dụng

Câu 1: Tìm giá trị của tham số m để đồ thị hàm số 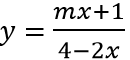nhận đường thẳng y = 1 làm tiệm cận ngang.

Lời giải:

Nghiệm của mẫu thức x = 2. Để đồ thị hàm số có tiệm cận thì x = 2 không là nghiệm của phương trình mx + 1 = 0 hay 2m + 1 ≠ 0 ⇔ m ≠ -1/2

Đường tiệm cận ngang của đồ thị hàm số là y = -m/2

Để đồ thị hàm số nhận y = 1 làm tiệm cận ngang thì -m/2 = 1 ⇔ m = -2 (thỏa mãn)

Vậy giá trị tham số m cần tìm là m = -2

Câu 2: Tìm giá trị của tham số m để đồ thị hàm số 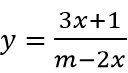nhận đường thẳng x = 1 làm tiệm cận đứng.

Lời giải:

Nghiệm của tử thức x = -1/3. Để đồ thị hàm số có tiệm cận thì x = -1/3 không là nghiệm của phương trình m - 2x = 0 hay m - 2.(-1/3) ≠ 0 ⇔ m ≠ -2/3

Đường tiệm cận đứng của đồ thị hàm số là x = m/2

Để đồ thị hàm số nhận x = 1 làm tiệm cận đứng thì m/2 = 1 ⇔ m = 2

Vậy giá trị tham số m cần tìm là m = 2

Câu 3: Cho hàm số 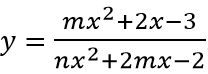. Đồ thị hàm số nhận đường thẳng x = 2; y = 2 lần lượt là tiệm cận đứng và tiệm cận ngang. Biểu thức 9m² + 6mn + 36n² có giá trị là bao nhiêu?

Lời giải:

Để x = 2 làm tiệm đứng của đồ thị hàm số thì x = 2 là nghiệm của mẫu nhưng không là nghiệm của tử hay

Để y = 2 làm tiệm cận ngang của đồ thị hàm số thì m/n = 2 ⇔ m = 2n

Giải hệ

Biểu thức 9m² + 6mn + 36n² = 9.(1/3)² + 6. 1/3.1/6 + 36.(1/6)² = 7/3

Câu 4:Tìm giá trị của m và n để đồ thị hàm số 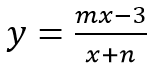nhận đường thẳng x = 2 làm tiệm cận đứng và đường thẳng y = 2 làm tiệm cận ngang.

Lời giải:

Để x = 2 làm tiệm đứng của đồ thị hàm số thì x = 2 là nghiệm của mẫu nhưng không là nghiệm của tử hay

Để y = 2 làm tiệm cận ngang của đồ thị hàm số thì m = 2

Vậy m = 2; n = -2

Câu 5: (Sở GD Bắc Giang 2017 L2). Tìm tập hợp các giá trị m để đồ thị hàm số 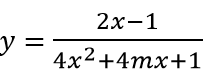có đúng một đường tiệm cận.

Lời giải:

Ta có nghiệm của tử thức x = 1/2

Vì 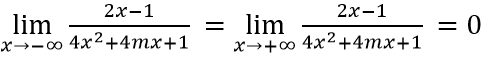⇒ y = 0 là tiệm cận ngang.

Để đồ thị hàm số có đúng một đường tiệm cận thì phương trình 4x^2+4mx+1=0 vô nghiệm hoặc có nghiệm kép và nghiệm đó bằng 1/2

Nếu phương trình 4x² + 4mx + 1 = 0 vô nghiệm ⇔ Δ' < 0 ⇔ 4m² - 4 < 0 ⇔ -1 < m < 1

Nếu phương trình 4x² + 4mx + 1 = 0 có nghiệm kép bằng -1/2

Vậy giá trị của tham số m cần tìm là -1 ≤ m < 1

Câu 6: (THPT Hai Bà Trưng – Huế 2017). Cho hàm số 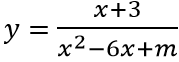. Tìm tất cả các giá trị tham số m để đồ thị hàm số chỉ có một tiệm cận đứng và một tiệm cận ngang.

Lời giải:

Ta có 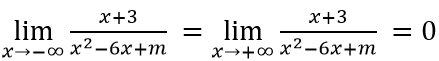⇒ y = 0 là tiệm cận ngang.

Nghiệm của tử thức x = -3

Để đồ thị hàm số chỉ có một tiệm cận đứng và một tiệm cận ngang thì x² - 6x + m = 0 chỉ có một nghiệm khác -3 hoặc có hai nghiệm phân biệt và một nghiệm bằng -3.

Trường hợp 1: Phương trình x² - 6x + m = 0 chỉ có một nghiệm khác -3

Trường hợp 2: Phương trình x² - 6x + m = 0 có hai nghiệm phân biệt và một nghiệm bằng -3.

Vậy giá trị của tham số m cần tìm là m = 9; m = -9.

Câu 7: (THPT Chuyên Phan Bội Châu – Nghệ An 2017 L3). Tìm các giá trị của tham số m sao cho đồ thị hàm số 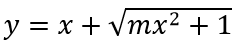có tiệm cận ngang.

Lời giải:

Nếu m = 0 thì y = x + 1. Suy ra đồ thị của nó không có tiệm cận ngang.

Nếu m < 0 thì hàm số xác định, ⇔ mx² + 1 ≥ 0 ⇔ (-1)/√(-m) ≤ x ≤ 1/√(-m)

Do đó, 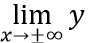không tồn tại nên đồ thị hàm số không có tiệm cận ngang.

Với 0 < m < 1 thì

nên đồ thị hàm số không có tiệm cận ngang.

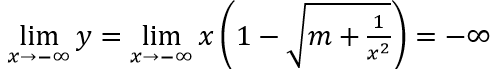
Với m = 1 thì

Suy ra đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số khi x → -∞

Với m>1 thì

nên đồ thị hàm số không có tiệm cận ngang.

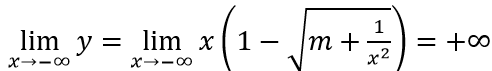
Vậy giá trị của tham số m cần tìm là m = 1

Câu 8: (THPT Chuyên ĐHSPHN 2017) Tìm tập hợp các giá trị thực của m để đồ thị hàm số

có đúng một đường tiệm cận.

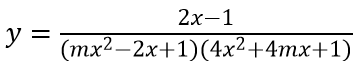
Lời giải:

Do 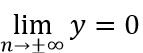nên đồ thị hàm số luôn có tiệm cận ngang y = 0. Để đây là tiệm cận duy nhất của đồ thị thì có hai trường hợp xảy ra

m = 0:) chỉ có tiệm cận ngang là y = 0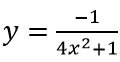

m ≠ 0, hai phương trình mx² - 2x + 1 = 0; 4x² + 4mx + 1 vô nghiệm. Tức là 1 - m < 0 và 4m² - 4 < 0 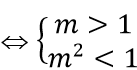(Vô lí)

Vậy không có giá trị m thỏa mãn