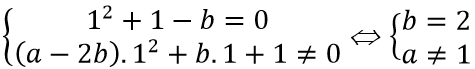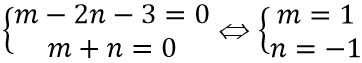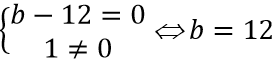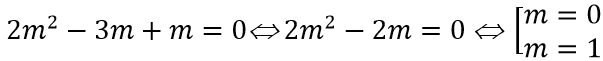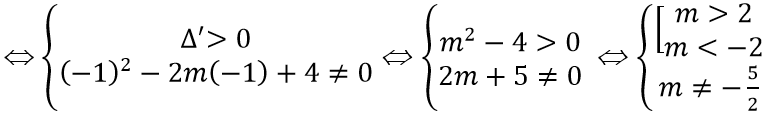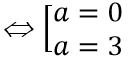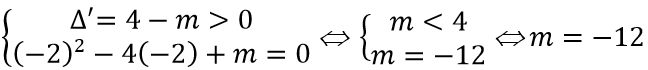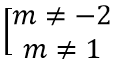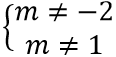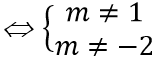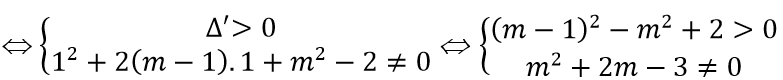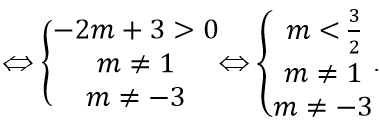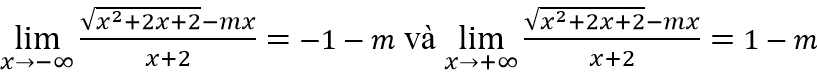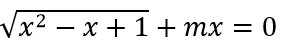Bài tập trắc nghiệm tìm tham số m để hàm số có tiệm cận cực hay - Toán lớp 12

---

Bài tập trắc nghiệm tìm tham số m để hàm số có tiệm cận cực hay

Với Bài tập trắc nghiệm tìm tham số m để hàm số có tiệm cận cực hay Toán lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm tham số m để hàm số có tiệm cận từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1: Biết đồ thị hàm số 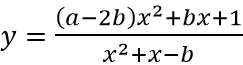có tiệm cận đứng là x = 1 và tiệm cận ngang là y = 0. Tính a + 2b

A. 6

B. 7

C. 8

D. 10

Lời giải:

Đáp án : C

Giải thích :

Vì đồ thị hàm số 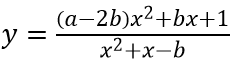nhận x = 1 làm tiệm cận đứng nên x = 1 là nghiệm của mẫu nhưng không là nghiệm của tử hay

Vì đồ thị hàm số có tiệm cận ngang y = 0 nên a - 2b = 0 ⇔ a = 2b = 4

Vậy a + 2b = 4 + 2.2 = 8.

Câu 2: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 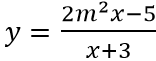nhận đường thẳng y = 8 làm tiệm cận ngang

A. m = 2

B. m = -2

C. m = ±2

D. m = 0

Lời giải:

Đáp án : C

Giải thích :

Do 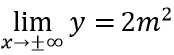nên đồ thị hàm số luôn có tiệm cận ngang y = 2m²

Cho 2m² = 8 ⇔ m = ±2.

Câu 3: Biết rằng đồ thị hàm số 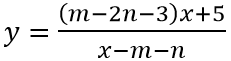nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng S = m² + n² - 2

A. S = 2

B. S = 0

C. S = -1

D. S = 1

Lời giải:

Đáp án : B

Giải thích :

Ta có hàm số 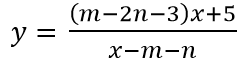là hàm phân thức nên nhận y = m - 2n - 3 là tiệm cận ngang và x = m + n là tiệm cận đứng của đồ thị hàm số.

Vì đồ thị hàm số nhận x = 0; y = 0 làm tiệm cận đứng và tiệm cận ngang nên ta có:

Khi đó S = m² + n² - 2 = 1 + 1 - 2 = 0.

Câu 4: (THPT Lý Thái Tổ - Hà Nội 2017 L4). Tìm m để đồ thị hàm số 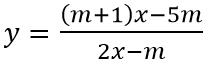có tiệm cận ngang là đường thẳng y = 1

A. m = 2

B. m = 5/2

C. m = 0

D. m = 1

Lời giải:

Đáp án : D

Giải thích :

Ta có hàm số 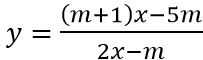là hàm phân thức nên nhận y = (m + 1)/2 là tiệm cận ngang.

Cho (m + 1)/2 = 1 ⇒ m = 1.

Câu 5: (THPT Triệu Sơn – Thanh Hóa 2017 L3). Biết đồ thị hàm số 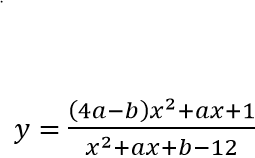nhận trục hoành và trục tung làm hai tiệm cận thì giá trị của a + b là:

A. 2

B. 10

C. 15

D. -10

Lời giải:

Đáp án : C

Giải thích :

Vì đồ thị hàm số 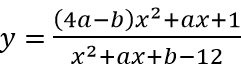nhận x = 0 làm tiệm cận đứng nên x = 0 là nghiệm của mẫu nhưng không là nghiệm của tử hay

Vì đồ thị hàm số nhận y = 0 làm tiệm cận ngang nên ta có 4a - b = 0 ⇒ a = b/4 = 3

Khi đó a + b = 15.

Câu 6: (Sở GD Hải Dương 2017). Biết đồ thị hàm số 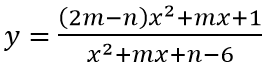nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m + n

A. 2

B. 8

C. -6

D. 9

Lời giải:

Đáp án : D

Giải thích :

Ta có:

= 2m - n, đồ thị hàm số nhận trục hoành làm tiệm cận khi và chỉ khi 2m - n = 0

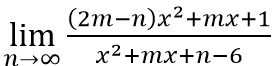
Do đồ thị hàm số nhận trục tung x = 0 làm tiệm cận nên x = 0 là nghiệm của x² + mx + n - 6 = 0. Suy ra n - 6 = 0

Do đó m = 3, n = 6 ⇒ m + n = 9.

Câu 7: Giá trị thực của tham số m để đồ thị hàm số 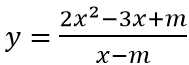không có tiệm cận đứng là:

A. m = 0

B. m = 1; m = 2

C. m = 0; m = 1

D. m = 1

Lời giải:

Đáp án : C

Giải thích :

Nghiệm của mẫu thức x = m. Để hàm số không có tiệm cận đứng thì:

Câu 8: Giá trị thực của tham số m để đồ thị hàm số 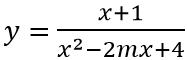có ba đường tiệm cận là:

A. m ∈ (-∞; -2) ∪ (2; +∞)

B. m ∈ (-∞; -5/2) ∪ (-5/2; -2)

C. m ∈ (-∞; -5/2) ∪ (-5/2; -2) ∪ (2; +∞)

D. m ∈ (2; +∞)

Lời giải:

Đáp án : C

Giải thích :

Ta có 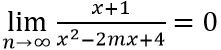⇒ y = 0 là tiệm cận ngang của đồ thị hàm số

Do đó yêu cầu bài toán 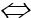phương trình x² - 2mx + 4 = 0 có hai nghiệm phân biệt khác -1.

Câu 9: Tất cả các giá trị thực của tham số a để đồ thị hàm số 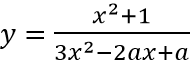có đúng một tiệm cận đứng.

A. a = ±√(3/2)

B. a = 0; a = 3

C. a = 1; a = 2

D. a = ±2

Lời giải:

Đáp án : B

Giải thích :

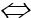
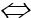
Yêu cầu bài toán 3x² - 2ax + a = 0 có nghiệm duy nhất Δ' = a² - 3a = 0

Câu 10: Tất cả các giá trị thực của tham số a để đồ thị hàm số 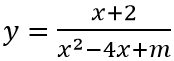có đúng một tiệm cận ngang và đúng một tiệm cận đứng.

A. m < 4

B. m > 4

C. m = 4; m = -12

D. m = 4

Lời giải:

Đáp án : C

Giải thích :

Ta có 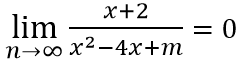nên y = 0 là tiệm cận ngang của đồ thị hàm số

Yêu cầu bài toán 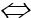phương trình x² - 4x + m = 0 có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng -2

Nếu x² - 4x + m = 0 có nghiệm kép thì Δ' = 4 - m = 0 ⇔ m = 4

Nếu x² - 4x + m = 0 có hai nghiệm phân biệt trong đó có một nghiệm bằng -2 thì

Vậy giá trị của tham số m cần tìm là m = 4; m = -12.

Câu 11: (THPT Sào Nam – Quảng Nam 2017). Cho hàm số 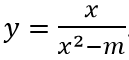. Giá trị của m để đồ thị hàm số có đúng 3 tiệm cận là:

A. m = 0

B. m < 0

C. m > 0

D. m ∈ R

Lời giải:

Đáp án : C

Giải thích :

Ta có 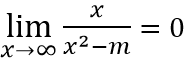nên y = 0 là tiệm cận ngang của đồ thị hàm số

Để đồ thị hàm số có đúng 3 tiệm cận thì phương trình x² - m = 0 ⇔ x² = m có hai nghiệm phân biệt khác 0 ⇔ m >0.

Câu 12: Giá trị thực của tham số m sao cho đồ thị hàm số 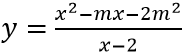có tiệm cận đứng

A. Không tồn tại m

B.

C. m ∈ R

D.

Lời giải:

Đáp án : D

Giải thích :

Nghiệm của mẫu thức x = 2

Để đồ thị hàm số 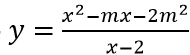có tiệm cận đứng thì x = 2 không phải là nghiệm của phương trình x² - mx - 2m² = 0

Khi đó ta có 2² - 2m - 2m² ≠ 0 ⇔ 2m² + 2m - 4 ≠ 0

Câu 13: Xác định giá trị của tham số m để đồ thị hàm số 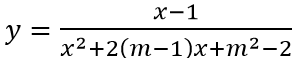có đúng hai tiệm cận đứng

A. m < 3/2; m ≠ 1; m ≠ -3

B. m > -3/2; m ≠ 1

C. m > -3/2

D. m < 3/2

Lời giải:

Đáp án : A

Giải thích :

Để đồ thị hàm số có hai tiệm cận đứng thì phương trình x² + 2(m - 1)x + m² - 2 = 0 có hai nghiệm phân biệt khác 1.

Xét

Để hàm số có hai tiệm cận ngang thì -1 - m ≠ 1 - m ⇔ -1 ≠ 1 (luôn đúng)

Câu 14: Đồ thị hàm số 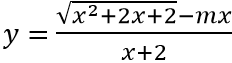có hai đường tiệm cận ngang khi

A. m ∈ R

B. m = 1

C. m = 0; m = 1

D. m = 0

Lời giải:

Đáp án : A

Câu 15: Đồ thị hàm số 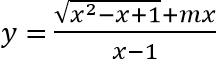có đường tiệm cận đứng khi

A. m ≠ 0     B. m ∈ R     C. m ≠ -1     D. m ≠ 1

Lời giải:

Đáp án : C

Giải thích :

Xét phương trình

Nếu phương trình không có nghiệm x = 1 thì đồ thị hàm số có đường tiệm cận đứng x = 1

Nếu phương trình có nghiệm x = 1 thì m = -1

Khi đó xét giới hạn 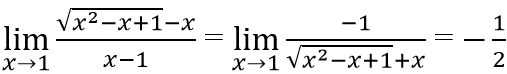nên trong trường hợp này đồ thị hàm số không có tiệm cận đứng.

Vậy m ≠ -1.