Tính F(x)=∫1+xsinx / cos^2 xdx . Chọn kết quả đúng
Câu hỏi:
Tính . Chọn kết quả đúng
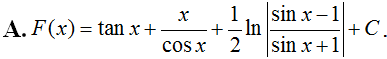
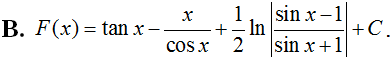
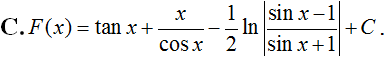
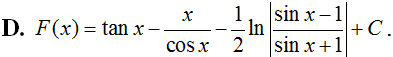
Trả lời:
Chọn A.
Biến đổi
Tính I(x) bằng cách đặt u=x;
Tính
Vậy
Câu hỏi:
Tính . Chọn kết quả đúng
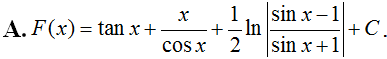
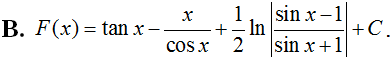
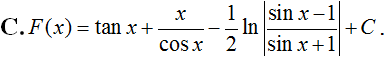
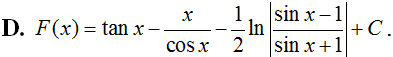
Trả lời:
Chọn A.
Biến đổi
Tính I(x) bằng cách đặt u=x;
Tính
Vậy
Câu 6:
Một nguyên hàm F(x) của hàm số thỏa mãn đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm nằm trên trục tung là:
Câu 7:
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 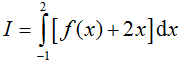 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
