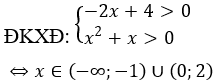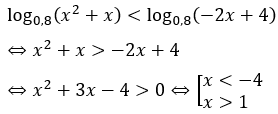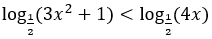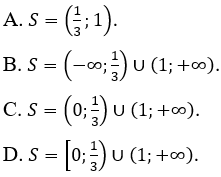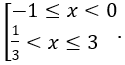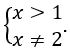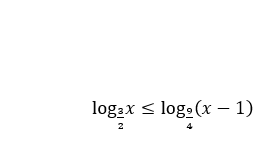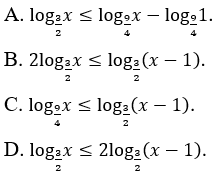Trắc nghiệm giải bất phương trình logarit bằng cách đưa về cùng cơ số - Toán lớp 12

---

Trắc nghiệm giải bất phương trình logarit bằng cách đưa về cùng cơ số

Với Trắc nghiệm giải bất phương trình logarit bằng cách đưa về cùng cơ số Toán lớp 12 tổng hợp 26 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải bất phương trình logarit bằng cách đưa về cùng cơ số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Giải bất phương trình log₂(3x-2) > log₂(6-5x) được tập nghiệm là (a; b). Hãy tính tổng S=a+b.

Lời giải:

Đáp án : D

Giải thích :

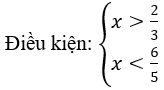
Ta có: log₂(3x-2) > log₂(6-5x) ⇔ 3x-2 > 6-5x ⇔ x > 1.

Giao với điều kiện ta được

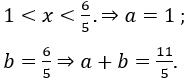
Bài 2: Có bao nhiêu số nguyên a là nghiệm bất phương trình log_0,5a ≤ log_0,5a² ?

A. 2.        B. 0.        C. Vô số.        D. 1.

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: a > 0.

Ta có: log_0,5a ≤ log_0,5a² ⇔ a ≥ a² ⇔ a²-a ≤ 0 ⇔ 0 ≤ a ≤ 1.

Giao với điều kiện ta được: 0 < a ≤ 1⇒ Bất phương trình có 1 nghiệm nguyên là a=1.

Bài 3: Tập nghiệm của bất phương trình log_0,2(x+1) > log_0,2(3-x)là

A. S=(1;3).        B. S=(1;+∈).        C. S=(-∈;1).        D. S=(-1;1).

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: -1 < x < 3.

Ta có: log_0,2(x+1) > log_0,2(3-x) ⇔ x+1 < 3-x ⇔ x < 1.

Giao với điều kiện ta được -1 < x < 1.

Bài 4: Tìm tập nghiệm của bất phương trình

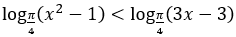
A. S=(1;2).        B. S=(-∈;-1)∪(2;+∈).

C. S=(-∈;1)∪(2;+∈).        D. S=(2;+∈).

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: x > 1.

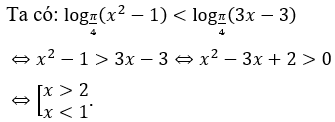
Giao với điều kiện ta được x > 2.

Bài 5: Bất phương trình sau có tập nghiệm là

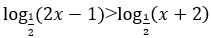
A. (3; +∈).        B. (-∈;3).        C. (1/2; 3).        D. (-2;3).

Lời giải:

Đáp án : C

Giải thích :

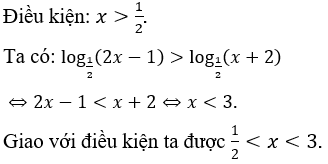
Bài 6: Tập nghiệm của bất phương trình log_0,8(x²+x) < log_0,8(-2x+4) là

A. (-∈;-4)∪(1;+∈).        B. (-4;1).        C. (-∈;-4)∪(1;2).        D.(1;2).

Lời giải:

Đáp án : C

Giải thích :

So sánh điều kiện ta có nghiệm :(-∈;-4)∪(1;2)

Bài 7: Tìm tập nghiệm S của bất phương trình

Lời giải:

Đáp án : C

Giải thích :

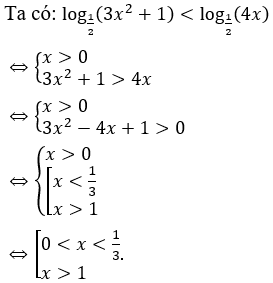
Bài 8: Tập nghiệm của bất phương trình ln(x²-3x+2) ≥ ln(5x+2) là

A. (-∈;0]∪[8;+∈).        B. [0;1)∪(2;8].        C. (-5/2;0]∪[8;+∈).        D. [8;+∈).

Lời giải:

Đáp án : C

Giải thích :

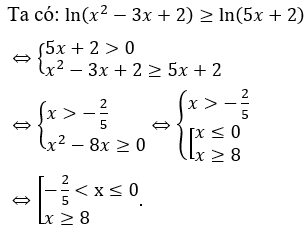
Bài 9: Bất phương trình log₄(x+7) > log₂(x+1) có tập nghiệm là

A. (1;4).        B. (5;+∈).        C. (-1; 2).        D. (-∈; 1).

Lời giải:

Đáp án : C

Giải thích :

Điều kiện: x > -1.

Khi đó:

log₄(x+7) > log₂(x+1) ⇔ log₄(x+7) > 2log₄(x+1) ⇔ log₄(x+7) > log₄(x+1)²

⇔ x+7 > x²+2x+1 ⇔ x²+x-6 < 0 ⇔ -3 < x < 2.

Giao với điều kiện ta được: -1 < x < 2.

Bài 10: Tập nghiệm của bất phương trình log₃x < log_√3(12-x) là

A. (0;12).        B. (9;16).        C. (0;9).        D. (0;16).

Lời giải:

Đáp án : C

Giải thích :

Điều kiện: 0 < x < 12.

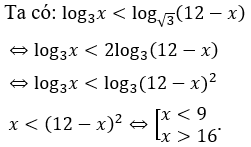
Giao với điều kiện ta được 0 < x < 9.

Bài 11: Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình. log_m(2x²+x+3) ≤ log_m(3x²-x). Biết rằng x=1 là một nghiệm của bất phương trình.

A. S=(-2;0)∪(1/3; 3 ].        B. S=(-1;0)∪(1/3; 2 ] .

C. S=[-1 ,0)∪(1/3; 3 ].        D. S=(-1;0)∪(1; 3 ].

Lời giải:

Đáp án : C

Giải thích :

Điều kiện: x < 0 ∨ x > 1/3.

Do x=1 là một nghiệm của bất phương trình nên ta có log_m6 ≤ log_m2 ⇔ 0 < m < 1.

Khi đó ta có:

log_m(2x²+x+3) ≤ log_m(3x²-x) ⇔ 2x²+x+3 ≥ 3x²-x ⇔ x²-2x-3 ≤ 0 ⇔ -1 ≤ x ≤ 3.

Giao với điều kiện ta được

Bài 12: Xác định tập nghiệm S của bất phương trình lnx² > ln(4x-4).

A. S=(2;+∈).        B. S=(1;+∈).        C. S=R\{2}.        D. S=(1;+∈)\{2}.

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: x > 1.

Ta có: lnx² > ln(4x-4) ⇔ x² > 4x-4 ⇔ x²-4x+4 > 0 ⇔ x ≠ 2.

Giao với điều kiện ta đươc:

Bài 13: Tập xác định của hàm số

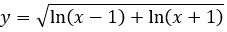
A. (1;+∈).        B. (-∈;√2).        C. ∅.        D. [√2;+∈).

Lời giải:

Đáp án : D

Giải thích :

Điều kiện xác định:

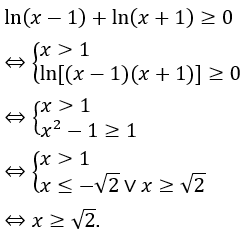
Bài 14: Bất phương trình sau tương đương với bất phương trình nào sau đây?

Lời giải:

Đáp án : B

Giải thích :

Điều kiện: 0 < x < 1.

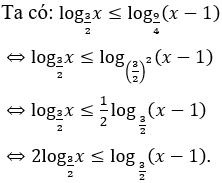
Bài 15: Giải bất phương trình log₃(3x-2) ≥ 2log₉(2x-1), ta được tập nghiệm là

A. (-∞;1).        B. (1;+∞).        C. (-∞;1].        D. [1;+∞).

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: x > 2/3.

Ta có: log₃(3x-2) ≥ 2log₉(2x-1) ⇔ 3x-2 ≥ 2x-1 ⇔ x ≥ 1 (Thỏa điều kiện)

Bài 16: Tất cả các giá trị của m để bất phương trình log₂(7x²+7) ≥ log₂(mx²+4x+m) có nghiệm đúng với mọi giá trị của x là

A. m ≤ 5.        B. 2 < m ≤ 5.        C. m ≥ 7.        D. 2 ≤ m ≤ 5.

Lời giải:

Đáp án : B

Giải thích :

Yêu cầu bài toán

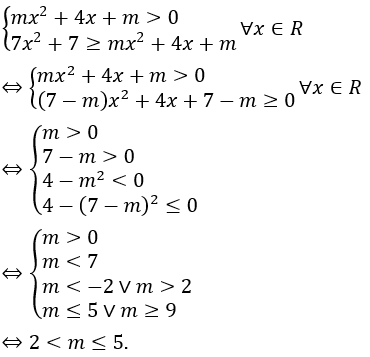
Bài 17: Có bao nhiêu số nguyên dương x thỏa mãn điều kiện log(x-40)+log(60-x) < 2?

A. 20.        B. 18.        C. 21.        D. 19.

Lời giải:

Đáp án : B

Giải thích :

Điều kiện: 40 < x < 60.

Ta có: log(x-40)+log(60-x) < 2 ⇔ log[(x-40)(60-x)] < 2 ⇔ (x-40)(60-x) < 100

⇔ -x²+100x-2500 < 0 ⇔ x ≠ 50.

Giao với điều kiện ta được tập nghiệm S=(40;60)\{50} ⇒ bất phương trình có 18 nghiệm nguyên.

Bài 18: Tìm tập nghiệm của bất phương trình log₂(x-3)+log₂x ≥ 2.

A. (3;+∞).        B. (-∞;-1]∪[4;+∞).        C. [4;+∞).        D. (3;4].

Lời giải:

Đáp án : C

Giải thích :

Điều kiện: x > 3.

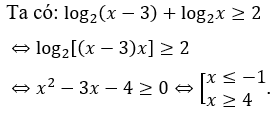
Giao với điều kiện ta đươc: x ≥ 4.

Bài 19: Tập nghiệm của bất phương trình 2log₂(x-1) ≤ log₂(5-x)+1 là

A. (1;5).        B. [1;3].        C. (1;3].        D. [3;5].

Lời giải:

Đáp án :C

Giải thích :

Điều kiện: 1 < x < 5.

Ta có: 2log₂(x-1) ≤ log₂(5-x)+1 ⇔ log₂(x-1)² ≤ log₂(10-2x) ⇔ (x-1)² ≤ 10-2x <

⇔ x²-9 ≤ 0 ⇔ -3 ≤ x ≤ 3.

Giao với điều kiện ta được: 1 < x ≤ 3.

Bài 20: Bất phương trình ssau là

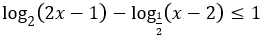
A. [3/4;+∞).        B. (3/4;+∞).        C. (3/4;3].        D. [3/4;3].

Lời giải:

Đáp án : C

Giải thích :

Điều kiện: x > 3/4.

Ta có: 2log₃(4x-3)+log_(1/3)(2x+3) ≤ 2 ⇔ log₃(4x-3)² ≤ log₃(2x+3)+log₃9

⇔ log₃(4x-3)² ≤ log₃(18x+27) ⇔ (4x-3)² ≤ 18x+27 ⇔ 16x²-42x-18 ≤ 0 ⇔ -3/8 ≤ x ≤ 3.

Giao với điều kiện ta được: 3/4 < x ≤ 3.

Bài 21: Bất phương trình log₂x+log₃x+log₄x > log₂₀x có tập nghiệm là

A. [1;+∞).        B. (0;1].        C. (0;1).        D. (1;+∞).

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: x > 0.

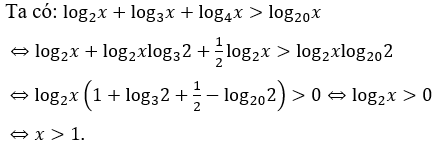
Bài 22: Tập nghiệm của bất phương trình log₂(x+2)-log₂(x-2) < 2

A. (10/3;+∞).        B. (-2;+∞).

C. (2;+∞).        D. (-2;2).

Lời giải:

Đáp án : A

Giải thích :

Điều kiện: x > 2.

Ta có: log₂(x+2)-log₂(x-2) < 2 ⇔ log₂(x+2) < log₂(x-2)+log₂4 ⇔ (x+2) < 4(x-2) ⇔ x > 10/3

Giao với điều kiện ta được: x > 10/3.

Bài 23: Tập nghiệm của bất phương trình log(x²+2x-3)+log(x+3)-log(x-1) < 0.

A. (-4;-2)∪(1;+∞).        B. (-2;1).        C. (1;+∞).        D. ∅.

Lời giải:

Đáp án : D

Giải thích :

Điều kiện: x > 1.

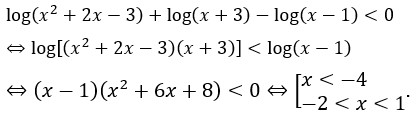
Giao điều kiện ta thấy bất phương trình vô nghiệm.

Bài 24: Bất phương trình sau có tập nghiệm là

A. (2,+∞).        B. (2,3].        C. (2,5/2].        D. [5/2,3].

Lời giải:

Đáp án : C

Giải thích :

Điều kiện: x > 2.

log₂(2x-1)-log_(1/2) (x-2) ≤ 1 ⇔ log₂(2x-1)+log₂(x-2) ≤ 1

⇔ log₂[(2x-1)(x-2)] ≤ 1

⇔ (2x-1)(x-2) ≤ 2 ⇔ 0 ≤ x ≤ 5/2.

Giao với điều kiện ta được: 2 < x ≤ 5/2.

Bài 25: Tìm tập nghiệm S của bất phương trình sau

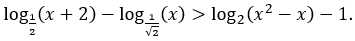
A. S=(2;+∞).        B. S=(1;2).        C. S=(0;2).        D. S=(1;2].

Lời giải:

Đáp án : B

Giải thích :

Điều kiện: x > 1.

Ta có:

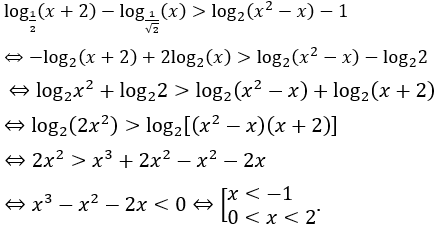
Giao với điều kiện ta được: 1 < x < 2.

Bài 26: Cho bất phương trình log_0,2x-log₅(x-2) < log_0,23. Nghiệm của bất phương trình đã cho là

A. x > 3.        B. 2 ≤ x < 3.        C. x ≥ 2.        D. 2 < x < 3.

Lời giải:

Đáp án : A

Giải thích :

Điều kiện: x > 2.

Ta có: log_0,2x-log₅(x-2) < log_0,23 ⇔ -log₅x-log₅(x-2)< -log₅3

⇔ log₅x+log₅(x-2) > log₅3 ⇔ log₅[x(x-2)] > log₅3 ⇔ x(x-2) > 3 ⇔ x²-2x-3 > 0

x < -1 ∨ x > 3.

Kết hợp điều kiện ta được: x > 3.