Trắc nghiệm giải bất phương trình logarit cơ bản - Toán lớp 12

---

Trắc nghiệm giải bất phương trình logarit cơ bản

Với Trắc nghiệm giải bất phương trình logarit cơ bản Toán lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải bất phương trình logarit cơ bản từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Giải bất phương trình log₃(2x-3) > 2

A. x > 3/2.        B. x > 6.        C. 3 < x < 6.        D. 3/2 < x < 6.

Lời giải:

Đáp án : B

Giải thích :

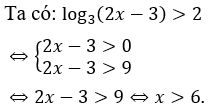
Bài 2: Nghiệm của bất phương trình log_√3(x-1) > 2 là

A. x < √3+1.        B. x > (√3)².        C. x > 4.        D. x ≤ 4.

Lời giải:

Đáp án : C

Giải thích :

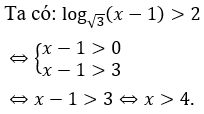
Bài 3: Bất phương trình sau có nghiệm là

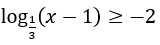
A.x > 1.        B.1 < x ≤ 10.        C.x ≥ 10.        D.1 ≤ x ≤ 10.

Lời giải:

Đáp án : B

Giải thích :

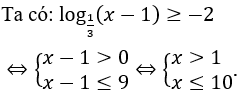
Bài 4: Số nghiệm nguyên của bất phương trình log(2x²-11x+25) ≤ 1 là

A. 5.        B. 6.        C. 7.        D. 8.

Lời giải:

Đáp án : D

Giải thích :

Ta có:

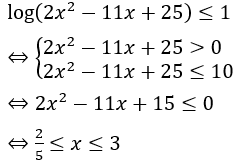
⇒ bất phương trình có 1 nghiệm nguyên

Bài 5: Nghiệm của bất phương trình log_0,3(3x-2) ≥ 0 là

A. (2;+∞).        B. (2/3;+∞).        C. (2/3;1).        D. (2/3;1].

Lời giải:

Đáp án : D

Giải thích :

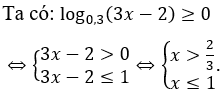
Bài 6: Tập xác định của hàm số

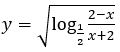
A. [0;2).        B. (0;2).        C. (-∞;-2)∪[0;2).        D. (-∞;-2).

Lời giải:

Đáp án : A

Giải thích :

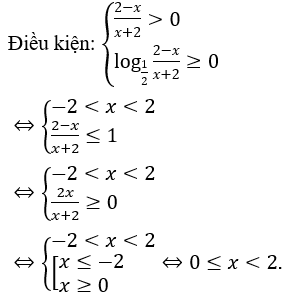
Bài 7: Tìm tập nghiệm S của bất phương trình

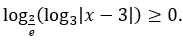
A. S=[0;2]∪[4;6].        B. S=[0;6].

C. S=[0;2)∪(4;6].        D. S=(-∞;0]∪[6;+∞).

Lời giải:

Đáp án : C

Giải thích :

Ta có:

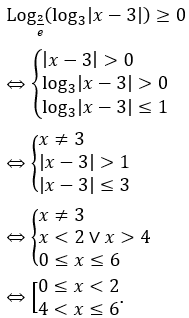
Bài 8: Nghiệm của bất phương trình sau là

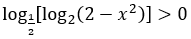
A. (-1;1)∪(2;+∞).        B. (-1;0)∪(0;1).        C. (-1;1).        D. (-∞;-1)∪(1;+∞)

Lời giải:

Đáp án : B

Giải thích :

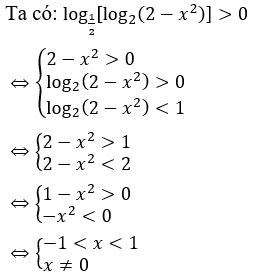
Bài 9: Giải bất phương trình sau trên tập số thực R.

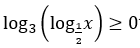
A. (0;1/2).        B. (0;1/2].        C. [1/4;1/2].        D. (0;1/4].

Lời giải:

Đáp án : B

Giải thích :

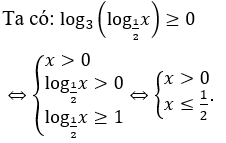
Bài 10: Tìm số nghiệm nguyên của bất phương trình log_√3-1(x²-2x+1) > 0 .

A. Vô số.        B. 0.        C. 2.        D. 1.

Lời giải:

Đáp án : B

Giải thích :

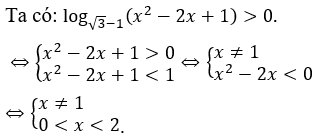
Bài 11: Tập nghiệm của bất phương trình ln[(x-1)(x-2)(x-3)+1] > 0 là

A. (1;2)∩(3;+∞).        B. (-∞;1)∪(2;3).        C. (-∞;1)∩(2;3).        D. (1;2)∪(3;+∞).

Lời giải:

Đáp án : D

Giải thích :

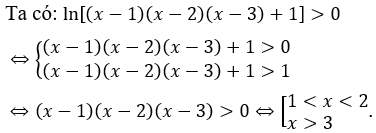
Bài 12: Giải bất phương trình

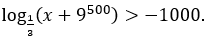
A. x < 0.        B. x > -9⁵⁰⁰.        C. x > 0.        D. -3¹⁰⁰⁰ < x < 0.

Lời giải:

Đáp án : D

Giải thích :

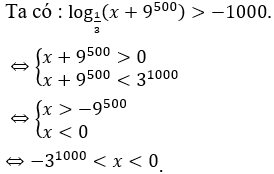
Bài 13: Bất phương trình sau có tập nghiệm là tập số thực R khi

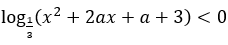
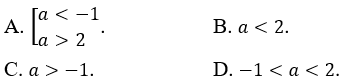
Lời giải:

Đáp án : D

Giải thích :

Ta có:

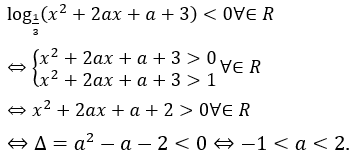
Bài 14: Tập nghiệm của bất phương trình 3 < log₂x < 4 là

A. (8;16).        B. (0;16).        C. (8;+∞).        D. R.

Lời giải:

Đáp án : A

Giải thích :

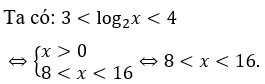
Bài 15: Số nghiệm thực nguyên của bất phương trình log(2x²-11x+15) ≤ 1 là

A. 3.        B. 4.        C. 5.        D. 6.

Lời giải:

Đáp án : B

Giải thích :

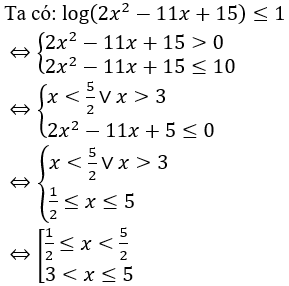
⇒ Bất phương trình có 4 nghiệm nguyên là 1,2,4,5.