Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;2;3), B (0;4;5)

Câu hỏi:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;2;3), B (0;4;5). Gọi M là điểm sao cho MA=2MB. Khoảng cách từ điểm M đến mặt phẳng (P): 2x - 2y - z + 6 = 0 đạt giá trị nhỏ nhất xấp xỉ là bao nhiêu?

A.1,12

B.1,17

C.1,21

D.1,22

Trả lời:

Chọn D

Gọi M (x;y;z).

Ta có MA = 2MB nên (x - 1)² + (y - 2)² + (z - 3)² = 4 [x² + (y - 4)² + (z - 5)²]

$\Leftrightarrow x^{2} + y^{2} + z^{2} + \frac{2}{3} x - \frac{28}{3} y - \frac{34}{3} z + 50 = 0$

Suy ra tập hợp các điểm M thỏa mãn MA = 2MB là mặt cầu (S) có tâm 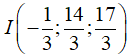và bán kính R = 2

Vì 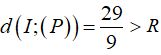nên (P) không cắt (S).

Do đó, khoảng cách từ điểm M đến mặt phẳng (P): 2x - 2y - z + 6 = 0 đạt giá trị nhỏ nhất là:

$d_{m i n} = d (I; (P)) - R = \frac{29}{9} - 2 = \frac{11}{9}$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng $d : \frac{x}{1} = \frac{y - 1}{1} = \frac{z - 2}{1}$ và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (S): x + 2y – 2z + 2018 = 0 và (Q): x + my + (m -1)z + 2017 = 0. Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng (Q)?

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau

$d_{1} : \{\begin{matrix} x = 4 - 2 t \\ y = t \\ z = 3 \end{matrix}, d_{2} : \{\begin{matrix} x = 1 \\ y = t' \\ z = - t' \end{matrix}$

Phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng trên là:

Xem lời giải »

Câu 4:

Trong không gian với tọa độ Oxyz, cho hai điểm A (1;1;2), B (-1; 3; -9). Tìm tọa độ điểm M thuộc Oy sao cho $△ A B M$ vuông tại M.

Xem lời giải »

Câu 5:

Cho tứ diện ABCD có M, N, P lần lượt thuộc các cạnh AB, BC, CD sao cho MA=MB, NB=2NC, PC=2PD. Mặt phẳng (MNP) chia tứ diện thành hai phần. Gọi T là tỉ số thể tích của phần nhỏ chia phần lớn. Giá trị của T bằng?

Xem lời giải »

Câu 6:

Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết điểm A (1; 2; 3), đường trung tuyến BM và đường cao CH có phương trình tương ứng là $\{\begin{matrix} x = 5 t \\ y = 0 \\ z = 1 + 4 t \end{matrix}$ và $\frac{x - 4}{16} = \frac{y + 2}{- 13} = \frac{z - 3}{5}$ . Viết phương trình đường phân giác góc A.

Xem lời giải »

Câu 7:

Trong không gian Oxyz cho điểm M (2;1;5). Mặt phẳng (P) đi qua điểm M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I (1;2;3) đến mặt phẳng (P)

Xem lời giải »

Câu 8:

Trong không gian (Oxy) cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là $\frac{x - 3}{- 1} = \frac{y - 3}{2} = \frac{z - 2}{- 1}$ , phương trình đường phân giác trong góc C là $\frac{x - 2}{2} = \frac{y - 4}{- 1} = \frac{z - 2}{- 1}$ . Biết rằng $\vec{u} = (m; n; - 1)$ là một véc tơ chỉ phương của đường thẳng AB. Tính giá trị biểu thức T=m²+n².

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;2;3), B (0;4;5)

Xem thêm bài tập Toán có lời giải hay khác: