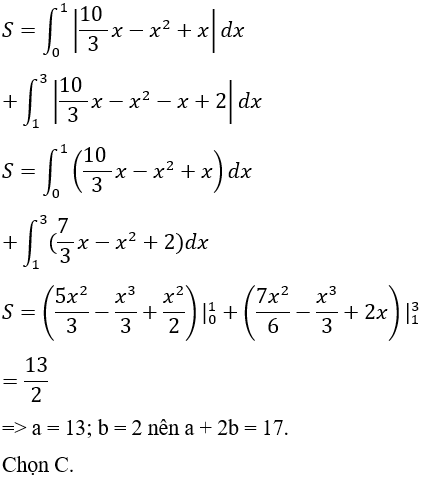Ứng dụng tích phân trong hình học - Tính diện tích hình phẳng - Toán lớp 12

---

Ứng dụng tích phân trong hình học - Tính diện tích hình phẳng

Với Ứng dụng tích phân trong hình học - Tính diện tích hình phẳng Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Ứng dụng tích phân trong hình học - Tính diện tích hình phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải

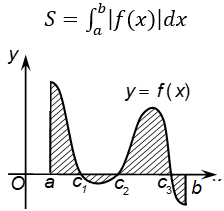
1. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x = a; x = b được xác định:

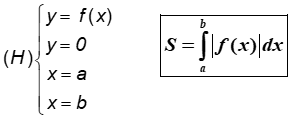
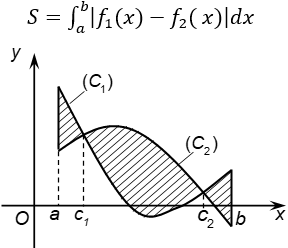
2. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f₁(x); y = f₂(x) liên tục trên đoạn [a;b] và hai đường thẳng x = a; x = b được xác định:

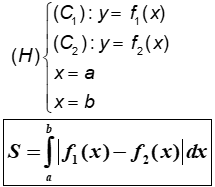
* Những điểm cần lưu ý:

    1. Nếu trên đoạn [a;b], hàm số y = f(x) không đổi dấu thì:

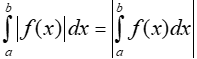
    2. Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối.

    3. Diện tích của hình phẳng giới hạn bởi các đường x = g(y); x = h(y) và hai đường thẳng y = c; y = d được xác định:

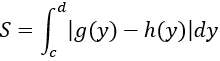
Trường hợp 1. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi các đường y = f(x) ; y = g(x); x = a; x = b là:

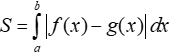
Phương pháp giải toán:

    +) Giải phương trình hoành độ giao điểm của hai đồ thị: f(x) = g(x) (1)

    +) Nếu (1) vô nghiệm thì:

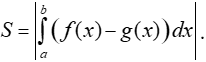
    +) Nếu (1) có nghiệm α thuộc [a;b] thì:

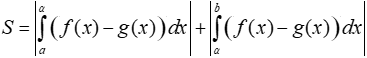
Chú ý: Có thể lập bảng xét dấu hàm số f(x) – g(x) trên đoạn [a;b] rồi dựa vào bảng xét dấu để tính tích phân.

Trường hợp 2. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi các đường y = f(x); y = g(x) là:

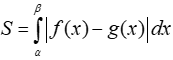
Trong đó α; β là nghiệm nhỏ nhất và lớn nhất của phương trình f(x) = g(x) (a ≤ α ≤ β ≤ b)

Phương pháp giải toán

    Bước 1. Giải phương trình hoành độ giao điểm f(x) = g(x) tìm các giá trị α; β.

    Bước 2. Tính 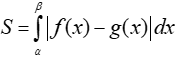như trường hợp 1.

B. Ví dụ minh họa

Ví dụ 1. Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần tô đậm trong hình) là:

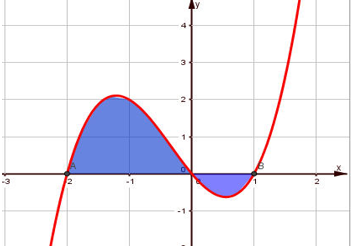
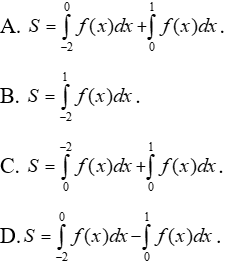
Lời giải

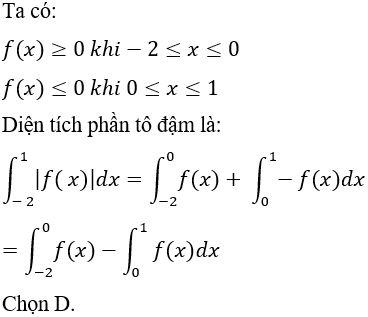
Ví dụ 2. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = x³, trục hoành và hai đường thẳng x = 1; x = 3 là:

A. 19.     B. 18.     C. 20.     D. 21.

Lời giải

Ví dụ 3. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = √x, trục hoành và hai đường thẳng x = 1; x = 4 là:

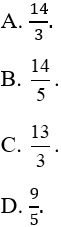
Lời giải

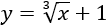
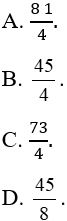
Ví dụ 4. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng x = 1; x = 8 là:

Lời giải

Ví dụ 5. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = sinx, trục hoành và hai đường thẳng 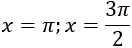là:

A. 1.     B. 1/2.     C. 2.     D. 3/2.

Lời giải

Ví dụ 6. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = -x² + 4, trục tung và trục hoành là:

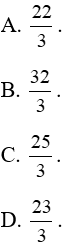
Lời giải

Ví dụ 7. Diện tích hình phẳng giới hạn bởi các đường (C₁): y = x³ + 11x - 6; (C₂): y = 6x²; x = 0; x = 2 (Đơn vị diện tích)

Lời giải

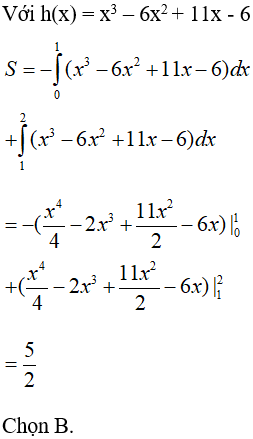
Ví dụ 8. Diện tích hình phẳng giới hạn bởi y = x³; y = 4x là:

A. 8.     B. 9.     C. 12.     D. 13.

Lời giải

Ví dụ 9. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = x⁴ - 3x² - 4, trục hoành và hai đường thẳng x = 0; x = 3 là:

Lời giải

Ví dụ 10. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = cos2x, trục hoành và hai đường thẳng 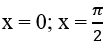là:

A. 2.     B. 1.     C. 3.     D. 4.

Lời giải

Ví dụ 11. Diện tích hình phẳng giới hạn bởi đường cong y = x³ - 4x, trục hoành và hai đường thẳng x = -3; x = 4 là:

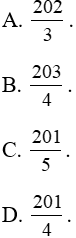
Lời giải

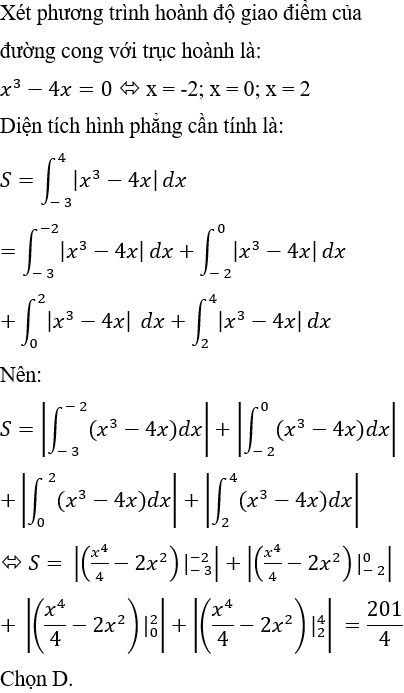
Ví dụ 12. Diện tích hình phẳng giới hạn bởi đường cong (C) y = xlnx, trục hoành và đường thẳng x = e là:

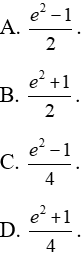
Lời giải

Ví dụ 13. Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số y = x² + x - 2; y = x + 2 và hai đường thẳng x = -2; x = 3. Diện tích của (H) bằng:

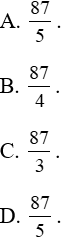
Lời giải

Ví dụ 14. Gọi (H) là hình phẳng được giới hạn bởi đồ thị hai hàm số y = (1 + e^x).x; y = (1 + e)x. Diện tích của (H) bằng:

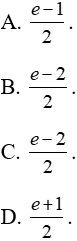
Lời giải

Ví dụ 15. Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số y = |x² - 1|; y = |x| + 5. Diện tích của (H) bằng:

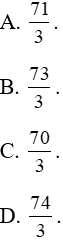
Lời giải

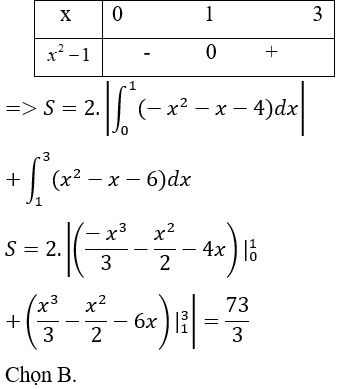
Ví dụ 16. Diện tích hình phẳng giới hạn bởi (P): y = x² + 3, tiếp tuyến của (P) tại điểm có hoành độ x = 2 và trục tung bằng:

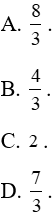
Lời giải

Ví dụ 17. Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y² – 2y + x = 0 và x + y = 0 là:

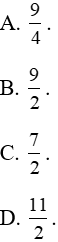
Lời giải

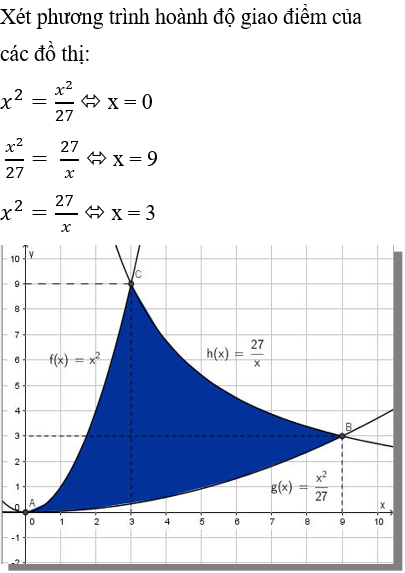
Ví dụ 18. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 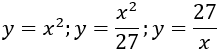bằng:

A. 27ln2.     B. 27ln3.     C. 28ln3.     D. 29ln3.

Lời giải

C. Bài tập vận dụng

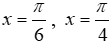
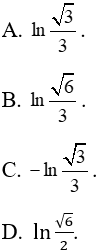
Câu 1: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = tanx, trục hoành và hai đường thẳng là:

Lời giải:

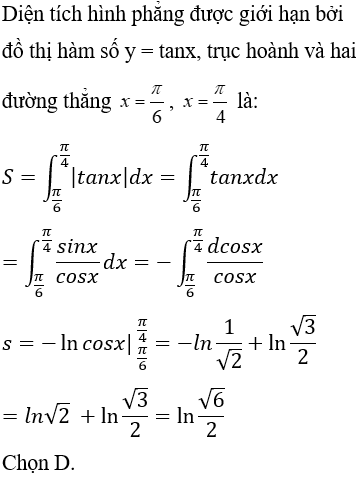
Câu 2: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = e^2x, trục hoành và hai đường thẳng x = 0, x = 1 là:

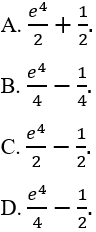
Lời giải:

Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = x³ - 3x², trục hoành và hai đường thẳng x = 1; x = 4 là:

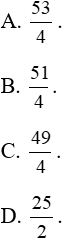
Lời giải:

Câu 4: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 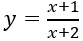, trục hoành và đường thẳng x = 2 là:

A. 3 + 2ln2.     B. 3 - ln2.     C. 3 - 2ln2.     D. 3 + ln2.

Lời giải:

Câu 5: Tính diện tích hình phẳng giới hạn bởi parabol y = 2 - x² và đường thẳng y = -x là:

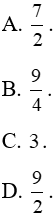
Lời giải:

Câu 6: Diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số y = 2x³ - 3x² + 1 và y = x³ - 4x² + 2x + 1 là:

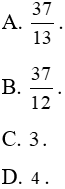
Lời giải:

Câu 7: Diện tích hình phẳng giới hạn bởi hai parabol 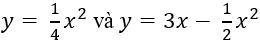là:

A. 7.     B. 8.     C. 9.     D. 6.

Lời giải:

Câu 8: Diện tích giới hạn bởi 2 đường cong: (C₁): y = x² + 1; (C₂): y = x² - 2x và đường thẳng x = -1 và x = 2.

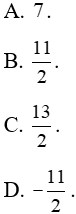
Lời giải:

Câu 9: Diện tích hình phẳng giới hạn bởi parabol: y = x² - 2x + 2 tiếp tuyến với parabol tại điểm M(3;5) và trục tung:

A. 7.     B. 6.     C. 5.     D. 9.

Lời giải:

Câu 10: Diện tích hình phẳng giới hạn bởi đường cong y = x(x – 1)(x – 2) và trục hoành:

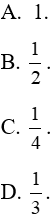
Lời giải:

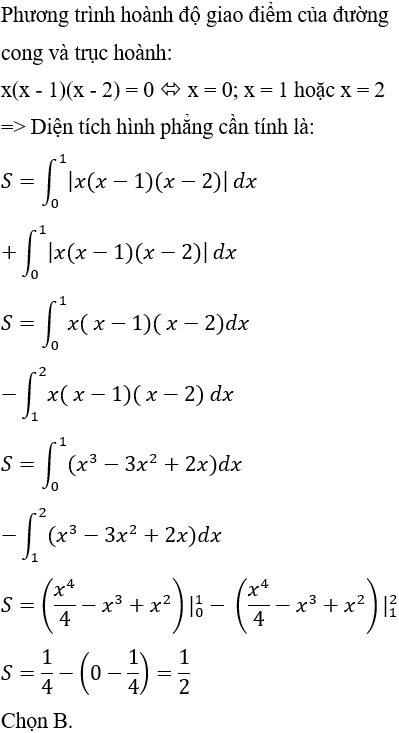
Câu 11: Diện tích hình phẳng trong hình vẽ sau là:

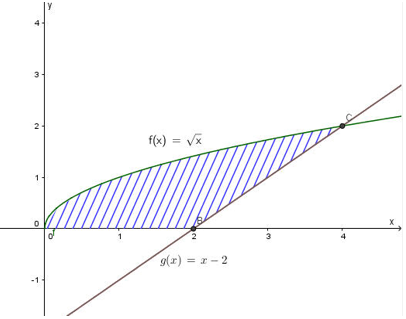
Lời giải:

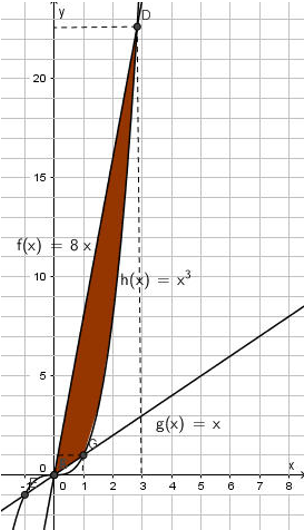
Câu 12: Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi các đường thẳng y = 8x; y = x và đồ thị hàm số y = x³ là a/b. Khi đó a + b bằng:

A. 68.    B. 67.    C. 66.     D. 65.

Lời giải:

Câu 13: Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1; y = x và đồ thị hàm số 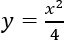trong miền x ≥ 0; y ≤ 1 là a/b. Khi đó b – a bằng:

A. 4.     B. 2.     C. 3.     D. 1.

Lời giải:

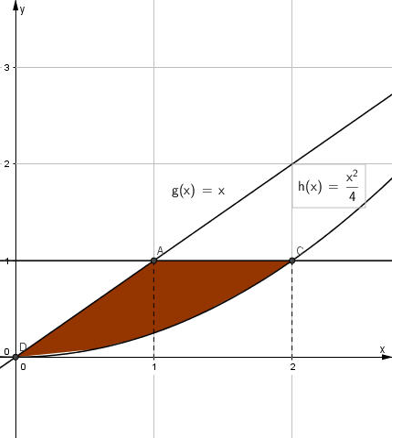
Câu 14: Diện tích hình phẳng giới hạn bởi các đường thẳng

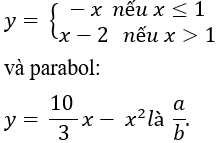
Khi đó a + 2b bằng:

A. 16.     B. 15.     C. 17.     D. 18.

Lời giải: