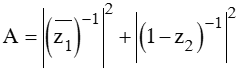Cho 2 số phức z1 = z^2 - (z ngang)^2/ z.z ngang + 1
Câu hỏi:
Cho 2 số phức 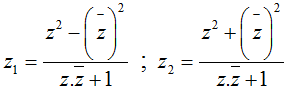 ; với z = x+ yi.
; với z = x+ yi.
Mệnh đề nào sau đây đúng?
A. z1 và z2 là số thuần ảo.
B. z2 là số thuần ảo.
C. z1 là số thuần ảo.
D. z1 và z2 là số thực.
Trả lời:
Chọn C.
Ta có: z = x+ yi nên z2 = x2 - y2 + 2xyi
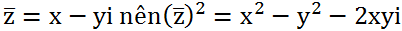
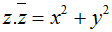
Khi đó : 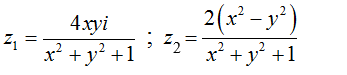
Suy ra z1 là số thuần ảo; z2 là số thuần thực.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
Xem lời giải »
Câu 2:
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
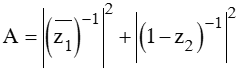
Xem lời giải »
Câu 3:
Gọi z1; z2 lần lượt là hai nghiệm của phương trình z2 – 4z + 7 = 0 .Tính giá trị của biểu thức 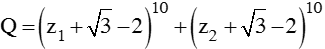
Xem lời giải »
Câu 4:
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
Xem lời giải »
Câu 5:
Cho ; . Tính
Xem lời giải »
Câu 7:
Cho số phức z thỏa mãn |z +1 +i | =| - 2i |. Tìm giá trị nhỏ nhất của |z|.
Xem lời giải »
Câu 8:
Tính tổng
Xem lời giải »
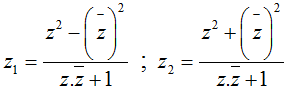 ; với z = x+ yi.
; với z = x+ yi.